%%html
<script src="https://bits.csb.pitt.edu/preamble.js"></script>
Review¶
CNN
- Receptive field size of kernel; successive applications expand field incrementally
- Good for identifying spatial, local features and learning hierarchy of features
RNN
- Receptive field is what it has seen so far
- But has trouble "remembering" what it has seen
- LSTM is better at remembering
Attention
- Receptive field is entire input
- Needs positional encoding to be position-specific (spatially aware)
Generative vs. Discriminative¶
A generative model produces as output the input of a discriminative model: $P(X|Y=y)$ or $P(X,Y)$
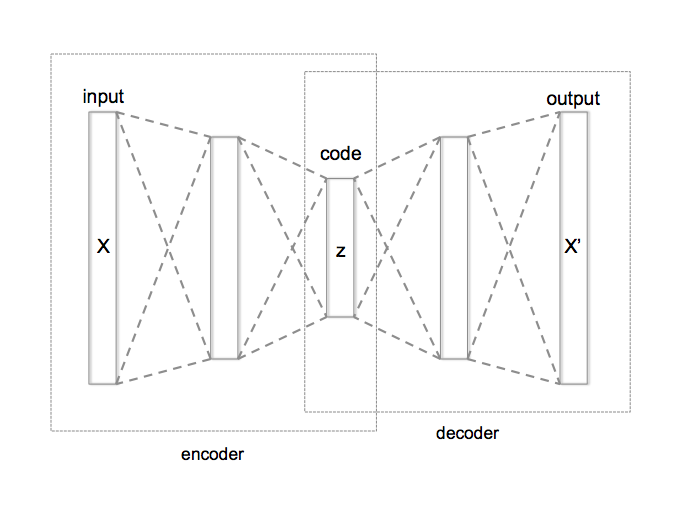
Autoencoders¶
Let's train an autoencoder on MNIST (input is 28x28).
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets
from torchvision import transforms
train_data = datasets.MNIST(root='../data', train=True,transform=transforms.ToTensor())
test_data = datasets.MNIST(root='../data', train=False,transform=transforms.ToTensor())
train_loader = torch.utils.data.DataLoader(train_data,batch_size=100,shuffle=True)
test_loader = torch.utils.data.DataLoader(test_data,batch_size=100,shuffle=False)
class MyAutoEncoder(nn.Module):
def __init__(self, latent_size): #initialize submodules here - this defines our network architecture
super(MyAutoEncoder, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=64, \
kernel_size=7, stride=1, padding=X)
self.conv2 = nn.Conv2d(in_channels=64, out_channels=64, \
kernel_size=7, stride=1, padding=X)
self.latent_size = latent_size
self.fc_encode = nn.Linear(3136, latent_size)
self.fc_decode1 = nn.Linear(latent_size, 500)
self.fc_decode2 = nn.Linear(500, 784)
def forward(self, x): # this actually applies the operations
inshape = x.shape
x = self.conv1(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = torch.flatten(x, 1)
x = latent = self.fc_encode(x)
x = F.softplus(self.fc_decode1(x)) #softplus is smooth approx of relu
x = F.softplus(self.fc_decode2(x))
return x.reshape(inshape), latent #return latent space representation
def generate(self,x):
with torch.no_grad():
batchsize = x.shape[0]
x = F.softplus(self.fc_decode1(x)) #softplus is smooth approx of relu
x = F.softplus(self.fc_decode2(x))
return x.reshape((batchsize,1,28,28))
%%html
<div id="whatpad" style="width: 500px"></div>
<script>
var divid = '#whatpad';
jQuery(divid).asker({
id: divid,
question: "What is X?",
answers: ["0","1","2","3","7"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
def train_ae(latent_size):
model = MyAutoEncoder(latent_size).to('cuda')
optimizer = torch.optim.Adam(model.parameters()) # need to tell optimizer what it is optimizing
losses = []
for epoch in range(10):
for i, (img,label) in enumerate(train_loader):
optimizer.zero_grad() # IMPORTANT!
img = img.to('cuda') #don't care about label!
output, latent = model(img)
loss = F.mse_loss(output,img)
loss.backward()
optimizer.step()
losses.append(loss.item())
if i % 1000 == 0:
print("epoch %d, iteration %d, loss %f"%(epoch,i,loss.item()))
return model,losses
%%time
model100, losses100 = train_ae(100)
epoch 0, iteration 0, loss 0.466085 epoch 1, iteration 0, loss 0.012018 epoch 2, iteration 0, loss 0.008846 epoch 3, iteration 0, loss 0.007461 epoch 4, iteration 0, loss 0.006674 epoch 5, iteration 0, loss 0.005437 epoch 6, iteration 0, loss 0.005378 epoch 7, iteration 0, loss 0.004438 epoch 8, iteration 0, loss 0.004234 epoch 9, iteration 0, loss 0.003591 CPU times: user 1min 9s, sys: 561 ms, total: 1min 10s Wall time: 1min 9s
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(losses100)
plt.ylim(0,.2);
from matplotlib import cm
def plot_imgs(model):
batch = next(iter(test_loader))
imgs = batch[0]
labels = batch[1]
genbatch, latent = model(imgs.to('cuda'))
genbatch = genbatch.detach().cpu().numpy() # remove from computation graph and move to CPU
fig,axes=plt.subplots(10,2,figsize=(4,20))
for i in range(10):
axes[i][0].imshow(genbatch[i][0],cmap=cm.Greys_r)
axes[i][1].imshow(imgs[i][0],cmap=cm.Greys_r)
axes[0][0].set_title('Generated')
axes[0][1].set_title('True');
return latent, labels
latent100, _ = plot_imgs(model100)
Latent Vector¶
latent100[0]
tensor([ 1.1821e+00, 2.7541e-01, 5.2303e-01, 5.2842e-01, 7.2577e-01,
-2.9952e+00, -2.8875e-01, 2.2576e-01, -2.9301e+00, 2.4102e-01,
-6.8178e+00, -2.5452e+00, -1.4065e+00, -4.5583e+00, -3.0011e+00,
-2.2526e+00, 1.2774e-01, 1.1715e+00, 3.4959e+00, -8.9686e-02,
-3.1287e-03, 7.3937e-01, -1.8150e+00, -2.5783e+00, -2.5707e+00,
2.7477e+00, 5.1790e+00, 2.7054e+00, -7.5436e-01, 2.3868e+00,
-2.4104e+00, 6.0113e+00, -7.5003e-01, -4.1176e+00, 4.0544e+00,
3.4794e+00, 1.5832e+00, 9.4781e-01, -1.4915e+00, -1.5748e+00,
-2.6026e+00, -1.6287e+00, 1.5664e-01, 1.3643e+00, -2.0033e+00,
-6.9889e+00, 1.3188e-01, 1.0948e-01, -2.0367e+00, 6.9195e-01,
2.3225e+00, -4.8781e+00, 3.3334e+00, -2.7200e+00, -2.5480e+00,
6.8248e-01, 3.1682e+00, 2.1084e+00, -3.4232e+00, 1.3786e+00,
-1.7187e+00, -1.0005e+00, -5.6148e-01, 1.5399e+00, 1.2128e+00,
2.1750e-01, 1.3939e+00, -1.1122e+00, -7.8315e-02, 3.1608e+00,
-5.9425e-02, 1.4927e+00, -2.2714e+00, 4.2443e+00, -1.6202e+00,
-7.5918e-02, 6.6270e-02, -4.6522e-01, 1.5404e+00, -4.8643e-02,
-4.1407e+00, 8.8498e-01, -1.0276e+00, -5.4198e+00, 1.6866e+00,
-1.7033e+00, -1.4342e+00, 1.0432e+00, 1.3793e+00, -2.4997e+00,
3.0524e-01, 4.1902e-01, -2.5756e-01, -8.7851e-01, -4.5882e-01,
6.1373e-01, -2.8110e+00, 9.3498e-01, -1.2536e+00, 1.4744e+00],
device='cuda:0', grad_fn=<SelectBackward0>)
%%html
<div id="redlat" style="width: 500px"></div>
<script>
var divid = '#redlat';
jQuery(divid).asker({
id: divid,
question: "What do you expect to happen if we reduce the size of the latent vector?",
answers: ["Smaller error","Similar error","Larger error"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
%%time
model10, losses10 = train_ae(10)
epoch 0, iteration 0, loss 0.461887 epoch 1, iteration 0, loss 0.022974 epoch 2, iteration 0, loss 0.017564 epoch 3, iteration 0, loss 0.018944 epoch 4, iteration 0, loss 0.018463 epoch 5, iteration 0, loss 0.017074 epoch 6, iteration 0, loss 0.015522 epoch 7, iteration 0, loss 0.016885 epoch 8, iteration 0, loss 0.015761 epoch 9, iteration 0, loss 0.016013 CPU times: user 1min 9s, sys: 182 ms, total: 1min 9s Wall time: 1min 7s
model2, losses2 = train_ae(2)
epoch 0, iteration 0, loss 0.493047 epoch 1, iteration 0, loss 0.050635 epoch 2, iteration 0, loss 0.047277 epoch 3, iteration 0, loss 0.048770 epoch 4, iteration 0, loss 0.050351 epoch 5, iteration 0, loss 0.048944 epoch 6, iteration 0, loss 0.049963 epoch 7, iteration 0, loss 0.048087 epoch 8, iteration 0, loss 0.050051 epoch 9, iteration 0, loss 0.046337
plt.plot(losses100,label='100')
plt.plot(losses10,label='10')
plt.plot(losses2,label='2')
plt.ylim(0,.2)
plt.legend();
latent,_ = plot_imgs(model10)
latent, labels = plot_imgs(model2)
import seaborn as sns
latent = latent.detach().cpu().numpy()
sns.scatterplot(x=latent[:,0],y=latent[:,1],hue=labels,palette='bright');
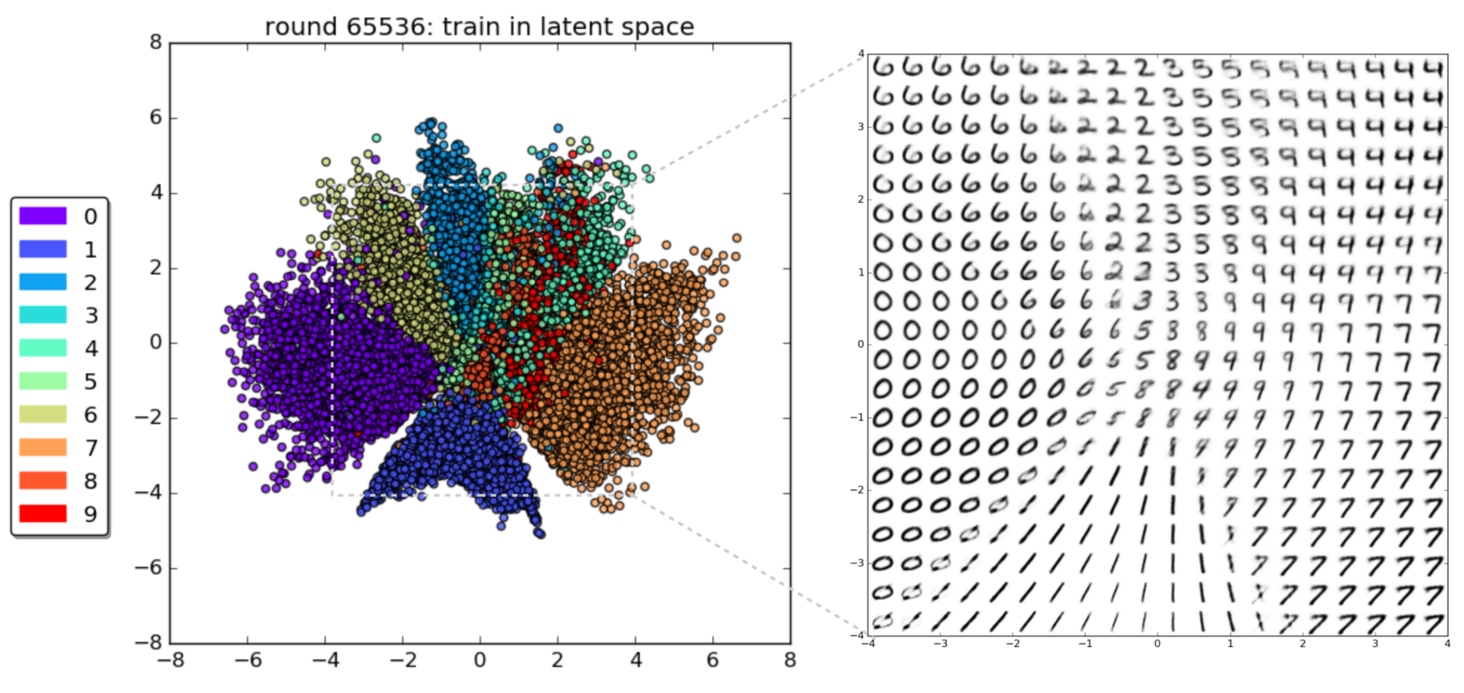
An autoencoder is dimensionality reduction technique¶
Our Latent Space¶
import numpy as np
l = latent100.detach().cpu().numpy()
diff = l[10]-l[0]
N = 10
L = torch.Tensor(np.array([l[0]+frac*diff for frac in np.linspace(0,1,N)]))
pi = model100.generate(L.to('cuda')).detach().cpu().numpy()
plt.figure(figsize=(16,4))
for i in range(N):
plt.subplot(1,N,i+1)
plt.imshow(pi[i].reshape((28,28)),cmap=cm.Greys_r)
Generating from Scratch¶
newL = torch.Tensor(np.random.normal(size=(5,100)))
pgen = model100.generate(newL.to('cuda')).cpu().numpy()
plt.figure(figsize=(10,4))
for i in range(5):
plt.subplot(1,5,i+1)
plt.imshow(pgen[i].reshape((28,28)),cmap=cm.Greys_r)
Variational Autoencoder¶
An autoencoder is good for constructing a compressed representation of the input. For generating new inputs, we want to impose some constraints on the latent space to make it more amenable to sampling.
http://kvfrans.com/variational-autoencoders-explained/
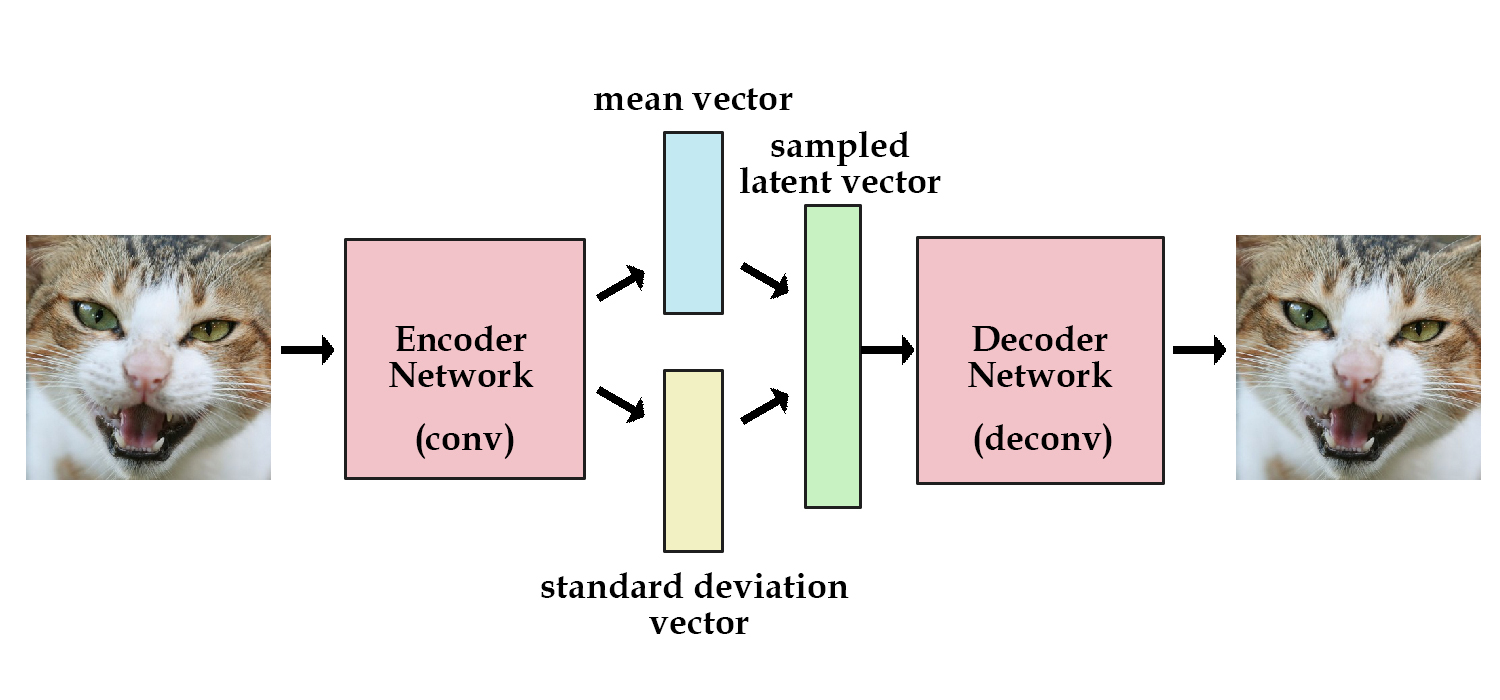
Reparameterization Trick¶
Problem: Sampling from a distribution is not differentiable.
Solution: Sample from $\mathcal{N}(0,1)$ (not differentiable) and scale (differentiable) by a predicted mean and standard deviation.
$$ \epsilon = \mathcal{N}(0,1) $$ $$ z = \mu + \sigma \cdot \epsilon$$
$z$ is now a sample from $\mathcal{N}(\mu,\sigma)$
Variational Autoencoder¶
Instead of generating the latent vector directly, we generate probability distributions from which the latent vector is sampled. To regularize this distributions we introduce a Kullback–Leibler divergence loss.
Kullback-Leibler divergence, $D_{KL}$ is a measure of how different two probability distributions are.
"A simple interpretation of the divergence of P from Q is the expected excess surprise from using Q as a model when the actual distribution is P."

%%html
<div id="klsame" style="width: 500px"></div>
<script>
var divid = '#klsame';
jQuery(divid).asker({
id: divid,
question: "Does KL(P||Q) == KL(Q||P)?",
answers: ["Yes","No"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Kullback-Leibler Divergence¶
"Usually, $P$ represents the data, the observations, or a measured probability distribution. Distribution $Q$ represents instead a theory, a model, a description or an approximation of $P$. The Kullback–Leibler divergence is then interpreted as the average difference of the number of bits required for encoding samples of $P$ using a code optimized for $Q$ rather than one optimized for $P$."
$$D_{\mathrm{KL}}\left( P || Q\right) = \int p(x)\log\left(\frac{p(x)}{q(x)}\right) dx = \mathbb{E}_p[ \log p(x) - \log q(x) ]$$
We will condition our generated distributions to be similar to a standard normal distribution.

%%html
<div id="whatisk" style="width: 500px"></div>
<script>
$('head').append('<link rel="stylesheet" href="https://bits.csb.pitt.edu/asker.js/themes/asker.default.css" />');
var divid = '#whatisk';
jQuery(divid).asker({
id: divid,
question: "What is k?",
answers: ["latent vector length","batch size","infinity","pixels"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Variational Autoencoder¶
Let's make our autoencoder variational...
class MyVAE(nn.Module):
def __init__(self, latent_size): #initialize submodules here - this defines our network architecture
super(MyVAE, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=64, kernel_size=7, stride=1, padding=X)
self.conv2 = nn.Conv2d(in_channels=64, out_channels=64, kernel_size=7, stride=1, padding=X)
self.latent_size = latent_size
self.fc_encode_mean = nn.Linear(3136, latent_size)
self.fc_encode_log_sigma_sq = nn.Linear(3136, latent_size)
self.fc_decode1 = nn.Linear(latent_size, 500)
self.fc_decode2 = nn.Linear(500, 784)
def forward(self, x): # this actually applies the operations
inshape = x.shape
x = self.conv1(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = torch.flatten(x, 1)
#two latent vectors
mean = self.fc_encode_mean(x)
log_sigma_sq = self.fc_encode_log_sigma_sq(x)
#sample according to mean/sigma
std = torch.exp(0.5*log_sigma_sq)
eps = torch.randn_like(std)
z = eps*std+mean
x = F.softplus(self.fc_decode1(z)) #softplus is smooth approx of relu
x = F.softplus(self.fc_decode2(x))
return x.reshape(inshape), (mean, log_sigma_sq, z) #return latent space representation
def generate(self,batchsize,std=1):
with torch.no_grad():
x = torch.normal(0, std,size=(batchsize,self.latent_size)).to('cuda')
x = F.softplus(self.fc_decode1(x)) #softplus is smooth approx of relu
x = F.softplus(self.fc_decode2(x))
return x.reshape((batchsize,1,28,28))
def train_vae(latent_size,mult=1):
model = MyVAE(latent_size).to('cuda')
optimizer = torch.optim.Adam(model.parameters()) # need to tell optimizer what it is optimizing
losses = []
for epoch in range(10):
for i, (img,label) in enumerate(train_loader):
optimizer.zero_grad() # IMPORTANT!
img = img.to('cuda') #don't care about label!
output, (mean, log_sigma_sq, z) = model(img)
l2loss = mult*F.mse_loss(output,img)
klloss = -0.5*torch.mean(torch.sum(\
1+log_sigma_sq - torch.square(mean) - \
torch.exp(log_sigma_sq),dim=1),dim=0)
loss = l2loss+klloss
loss.backward()
optimizer.step()
losses.append(loss.item())
if i % 1000 == 0:
print("epoch %d, iteration %d, losses %f = %f + %f"%\
(epoch,i,loss.item(),l2loss.item(),klloss.item()))
return model,losses
%%time
model100,losses100 = train_vae(100)
epoch 0, iteration 0, losses 0.778504 = 0.506249 + 0.272255 epoch 1, iteration 0, losses 0.065730 = 0.065730 + -0.000000 epoch 2, iteration 0, losses 0.067433 = 0.067433 + 0.000000 epoch 3, iteration 0, losses 0.066223 = 0.066223 + 0.000000 epoch 4, iteration 0, losses 0.066709 = 0.066709 + 0.000000 epoch 5, iteration 0, losses 0.067264 = 0.067264 + 0.000000 epoch 6, iteration 0, losses 0.071659 = 0.071659 + 0.000000 epoch 7, iteration 0, losses 0.068089 = 0.068088 + 0.000001 epoch 8, iteration 0, losses 0.065957 = 0.065956 + 0.000001 epoch 9, iteration 0, losses 0.068220 = 0.068219 + 0.000000 CPU times: user 1min 14s, sys: 259 ms, total: 1min 14s Wall time: 1min 12s
genimgs = model100.generate(10).cpu().numpy()
fig, axes = plt.subplots(1,10,figsize=(16,4))
for i in range(10):
axes[i].imshow(genimgs[i][0],cmap=cm.Greys_r)
latent, labels = plot_imgs(model100);
plt.hist(latent[2].detach().cpu().numpy().flatten(),bins=100,label='z');
Posterior Collapse!¶
The posterior (our desired distribution) has "collapsed" onto the prior distribution we are fitting with the KL divergence loss.
How to fix?
%%time
model100,losses100 = train_vae(100,1000)
epoch 0, iteration 0, losses 489.381409 = 489.018707 + 0.362690 epoch 1, iteration 0, losses 55.710548 = 49.215897 + 6.494653 epoch 2, iteration 0, losses 50.112415 = 40.437679 + 9.674735 epoch 3, iteration 0, losses 46.108665 = 36.279514 + 9.829151 epoch 4, iteration 0, losses 43.777828 = 34.007973 + 9.769855 epoch 5, iteration 0, losses 40.536324 = 29.290428 + 11.245897 epoch 6, iteration 0, losses 39.444569 = 28.167974 + 11.276593 epoch 7, iteration 0, losses 42.040955 = 30.187609 + 11.853347 epoch 8, iteration 0, losses 41.522102 = 29.518663 + 12.003438 epoch 9, iteration 0, losses 42.298878 = 29.080904 + 13.217975 CPU times: user 1min 15s, sys: 210 ms, total: 1min 15s Wall time: 1min 12s
latent, labels = plot_imgs(model100);
genimgs = model100.generate(10).cpu().numpy()
fig, axes = plt.subplots(1,10,figsize=(16,4))
for i in range(10):
axes[i].imshow(genimgs[i][0],cmap=cm.Greys_r)
plt.hist(latent[2].detach().cpu().numpy().flatten(),bins=100,label='z');
Generative Models of the Cell¶
https://arxiv.org/pdf/1705.00092.pdf
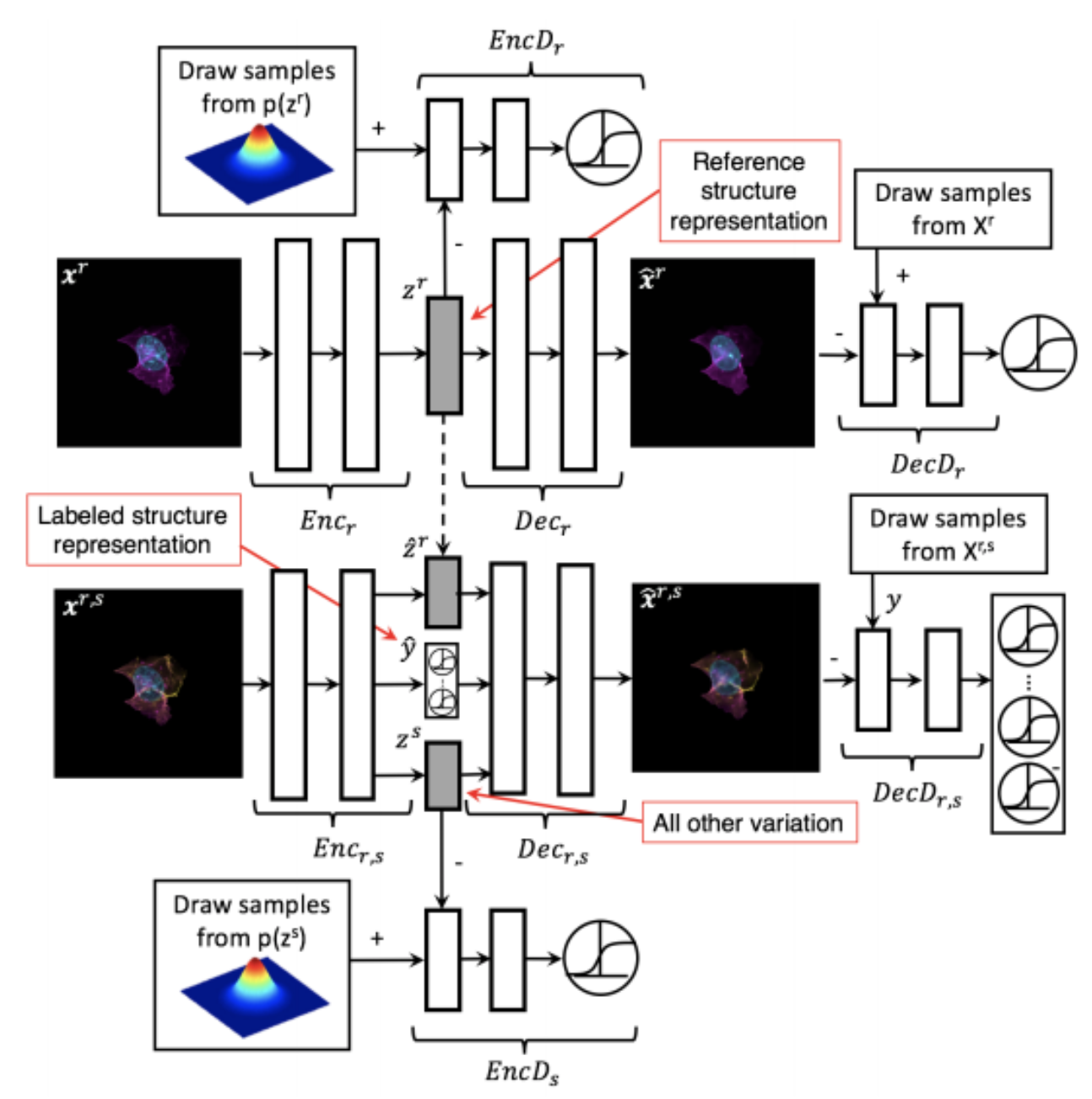
|
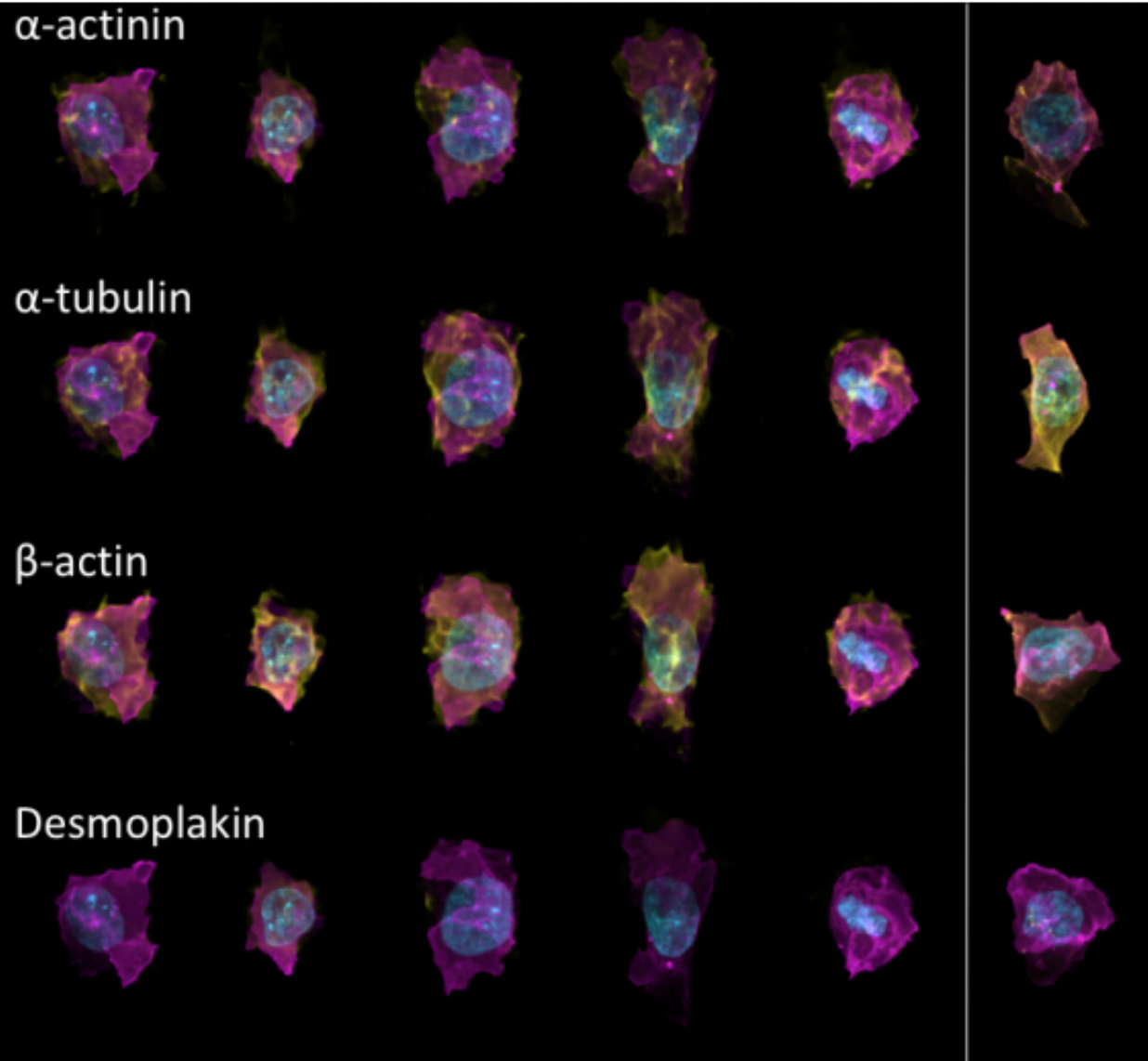
|
https://drive.google.com/file/d/0B2tsfjLgpFVhMnhwUVVuQnJxZTg/view
Generative Adversarial Networks¶
https://arxiv.org/abs/1406.2661
 https://youtu.be/G06dEcZ-QTg
https://youtu.be/G06dEcZ-QTg
Training a GAN¶
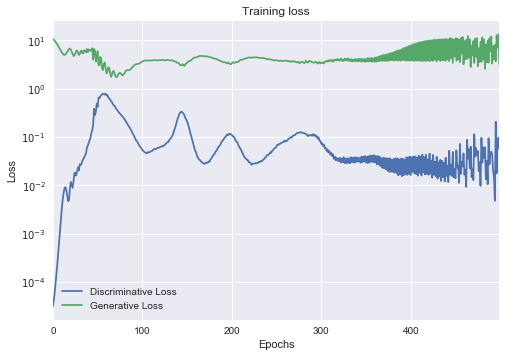
The loss is not necessarily a good indicator and for now, the most reliable way to check if their output makes sense is to put the output in front of an actual person. http://www.rricard.me/machine/learning/generative/adversarial/networks/keras/tensorflow/2017/04/05/gans-part2.html
https://towardsdatascience.com/gan-ways-to-improve-gan-performance-acf37f9f59b
An abbreviated GAN Tour¶
https://machinelearningmastery.com/tour-of-generative-adversarial-network-models/
We often want to condition our generated inputs in some way.
Conditional GAN¶
Both the discriminator and generator are conditioned on some variable (e.g., for MNIST we might condition on the label).
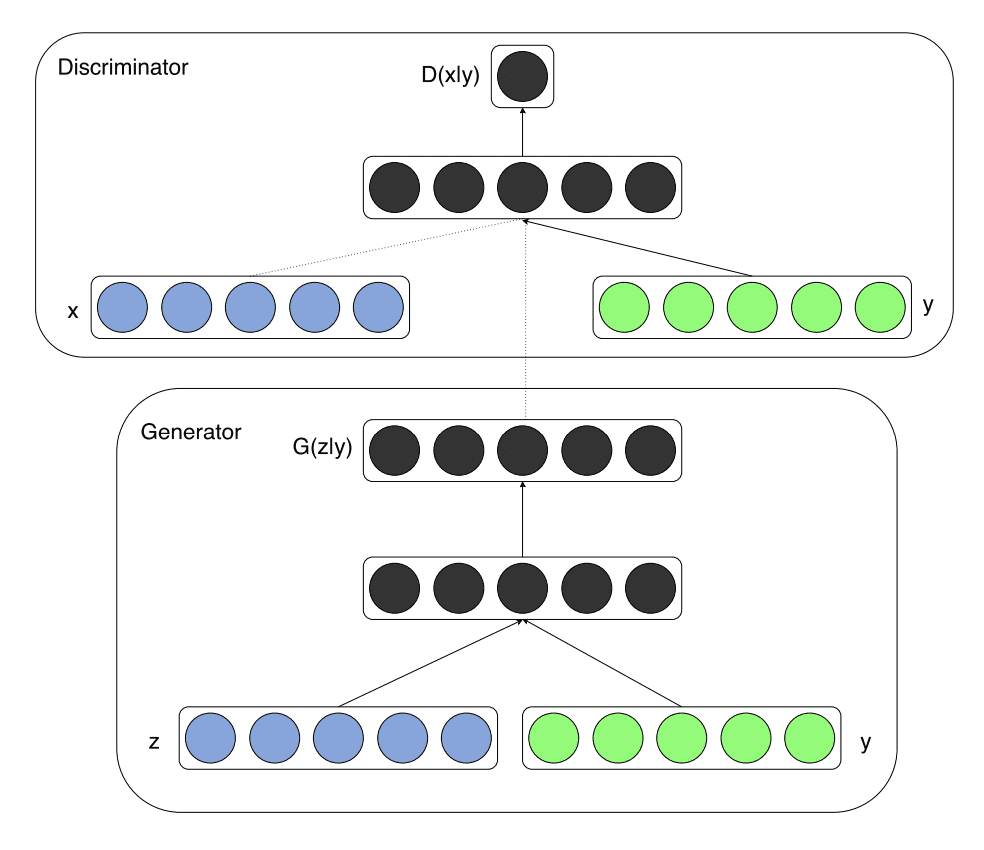
InfoGAN¶
You do not need to know what the labels are, only that there are labels (or other conditional properties). A network Q is expected to predict the conditional variable (label) used to generate the image from the image.

CycleGAN¶
Unlike pix2pix, you do not need matched pairs to convert between image domains.
https://medium.com/coding-blocks/introduction-to-cyclegans-1dbdb8fbe781



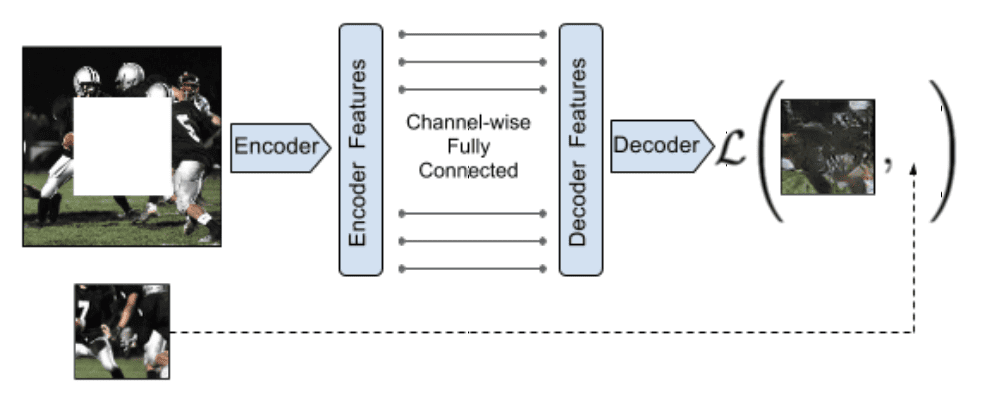
Context Encoders¶
The missing part of a picture is filled in. The doesn't have to use a GAN, but in practice an adversarial loss improves the result.

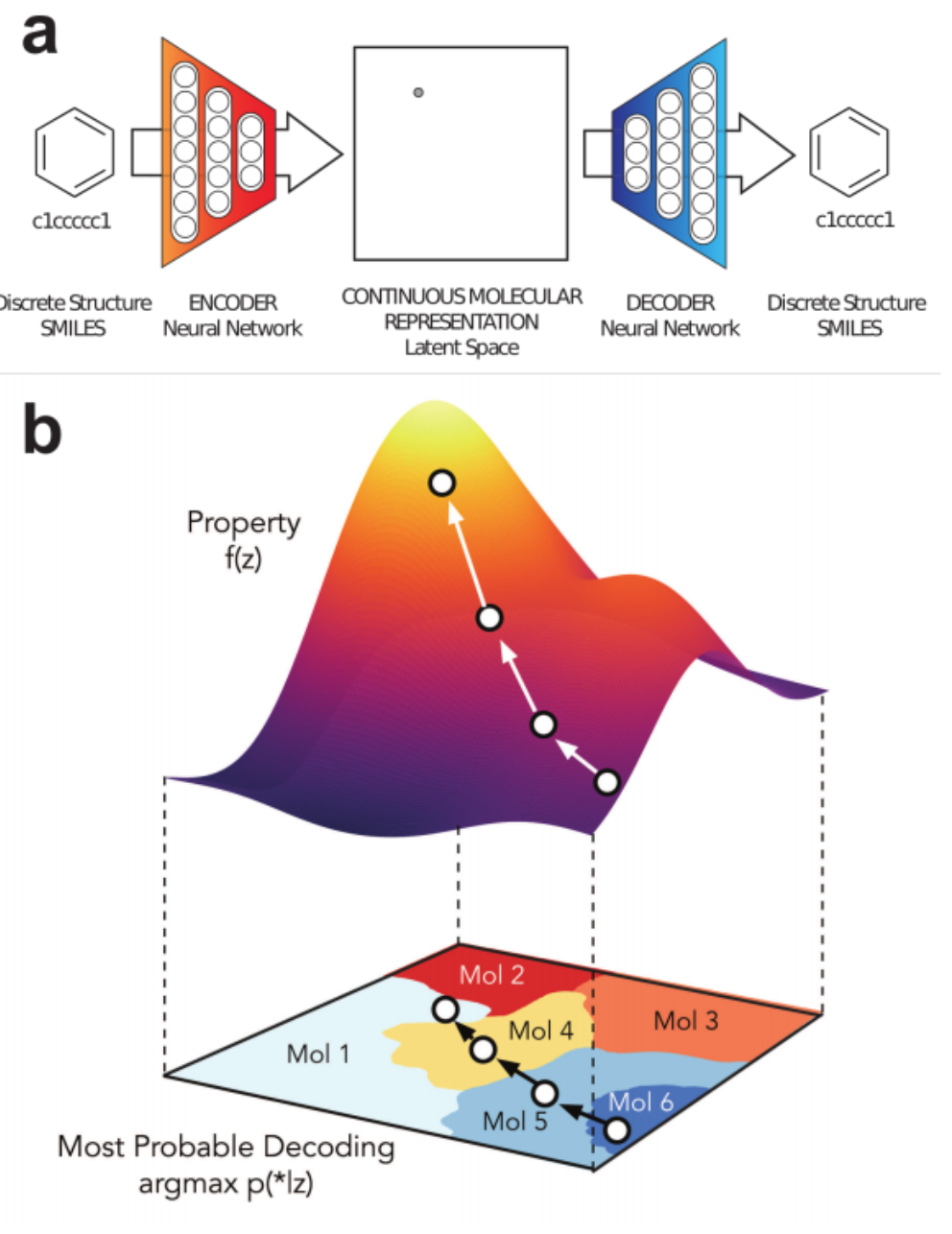 1% - 70% of output valid SMILES
1% - 70% of output valid SMILES