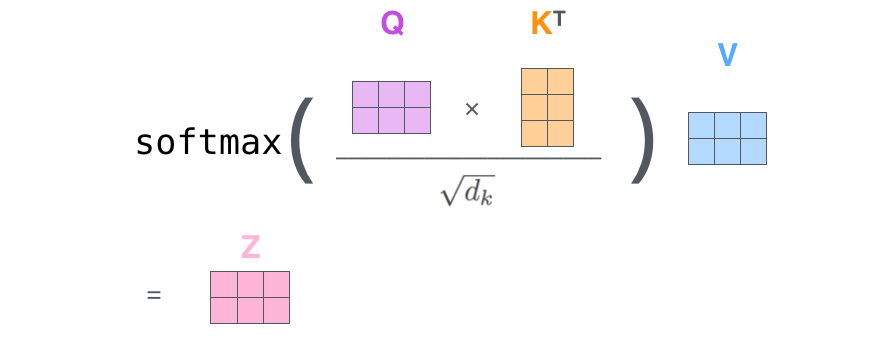Transformative Deep Learning

2/27/2024

print view

%%html
<script src="https://bits.csb.pitt.edu/preamble.js"></script>

Quiz Questions?

Assignment Questions

• How many workers?
• After calling data = dask.dataframe.read_table(...), what should data.npartitions be?
• What should npartitions be on the array provided to xgboost (if you've set it to use multiple threads)?
• How many times should you call compute (and when)?
• How many times should you call repartition? rechunk?
• Is your code that works on a regular pandas dataframe as fast as possible?

Recall RNNs

Attention

https://towardsdatascience.com/the-fall-of-rnn-lstm-2d1594c74ce0

“Drop your RNN and LSTM, they are no good!”

• RNNs struggle with long range dependencies
• RNNs are inherently sequential

Attention Mechanism

https://distill.pub/2016/augmented-rnns/#attentional-ex2

https://arxiv.org/pdf/1409.0473.pdf

They understand not, why Europe theoretically zwar exists, but not in reality

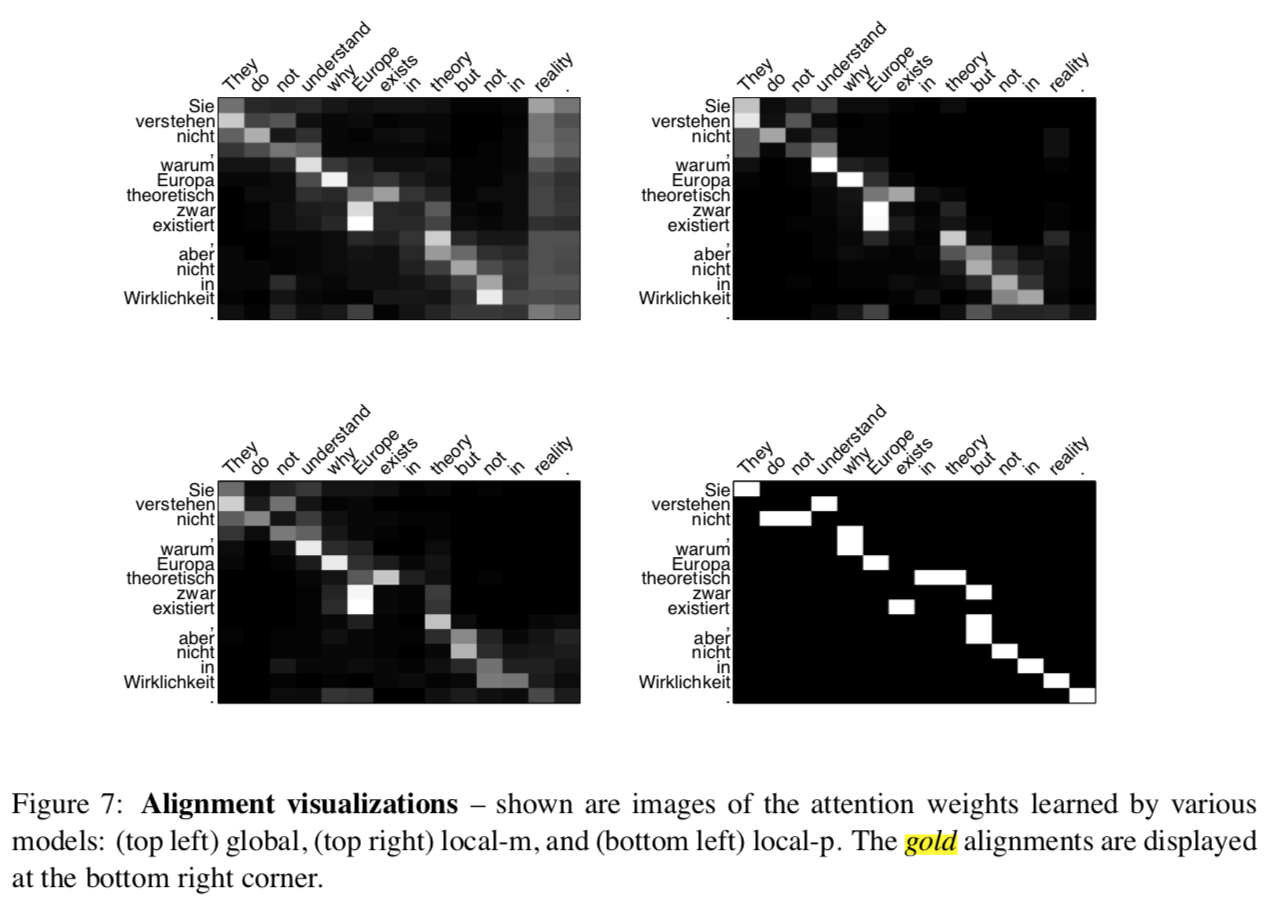
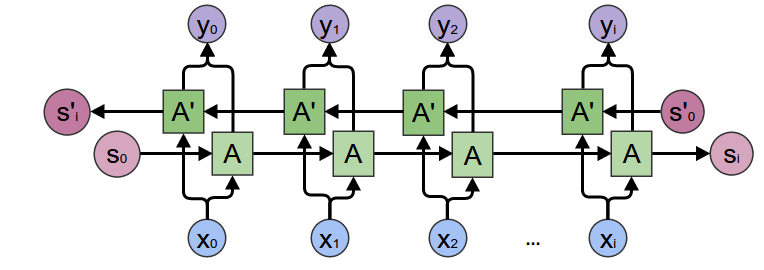
Attention vs Sequence-to-Sequence

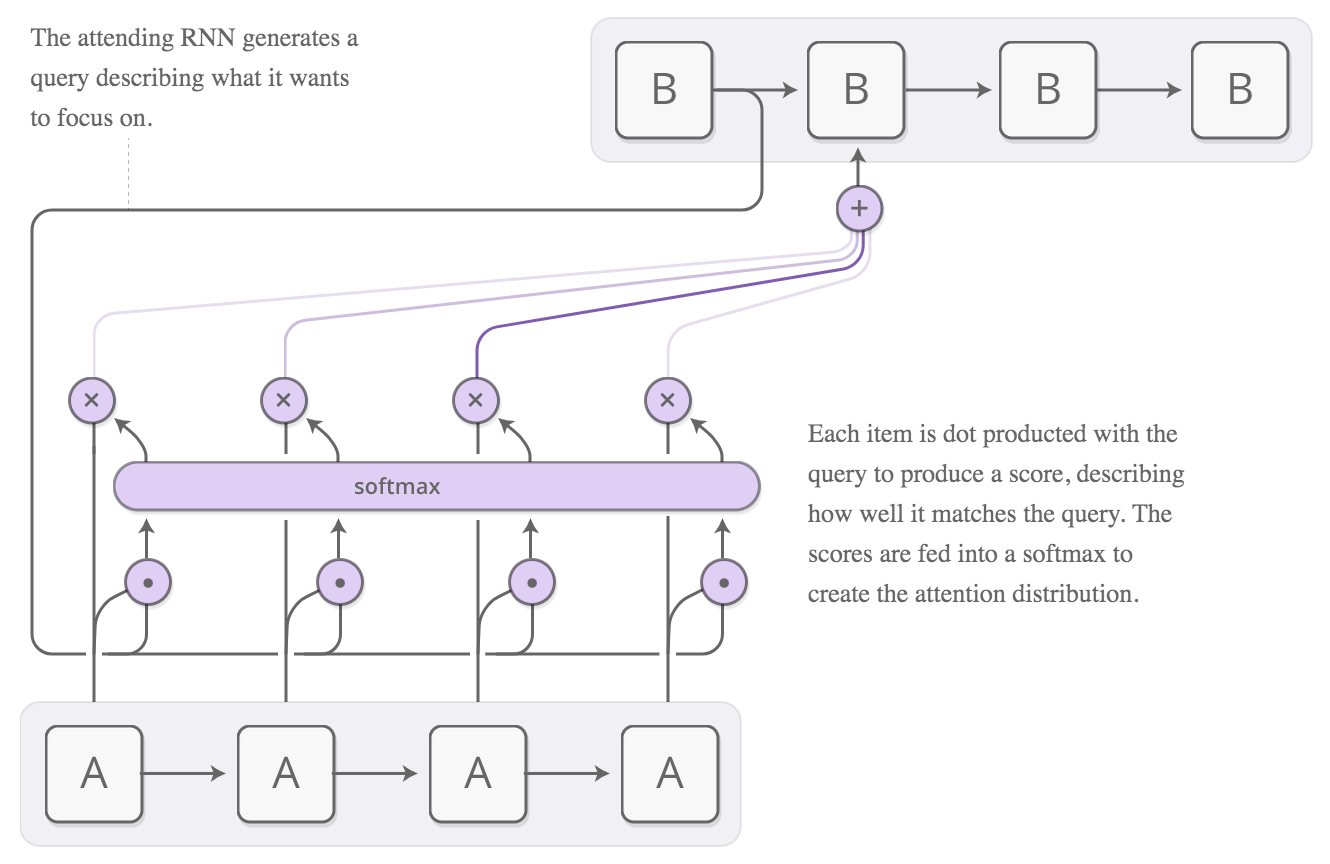
Instead of having to decode the result from a single hidden state vector, the decoder has access to all the hidden state vectors.

The attention mechanism determines which hidden states it uses for its output.

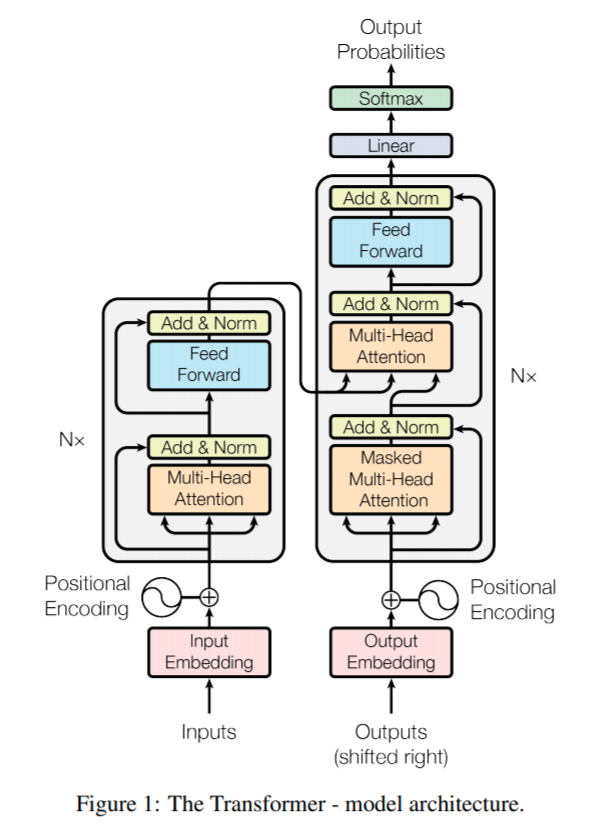
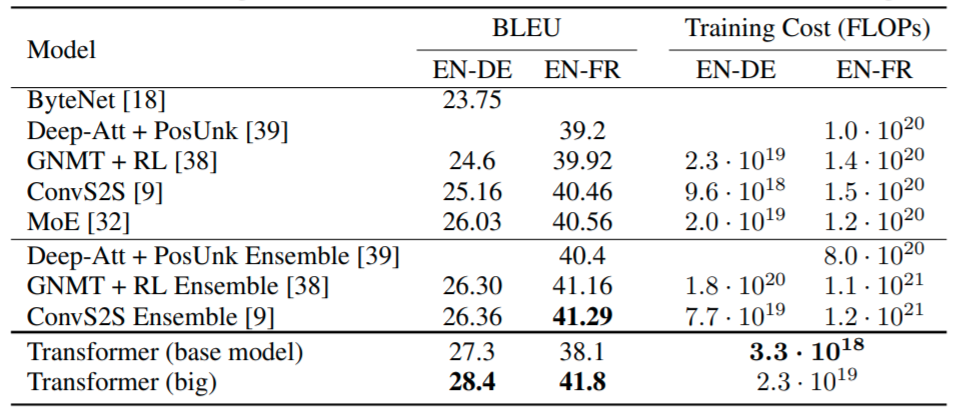
Transformers

Attention Is All You Need: https://arxiv.org/abs/1706.03762

http://jalammar.github.io/illustrated-transformer/

No recurrence (or convolution). Essentially each word is processed in parallel.

Context is learned via self-attention

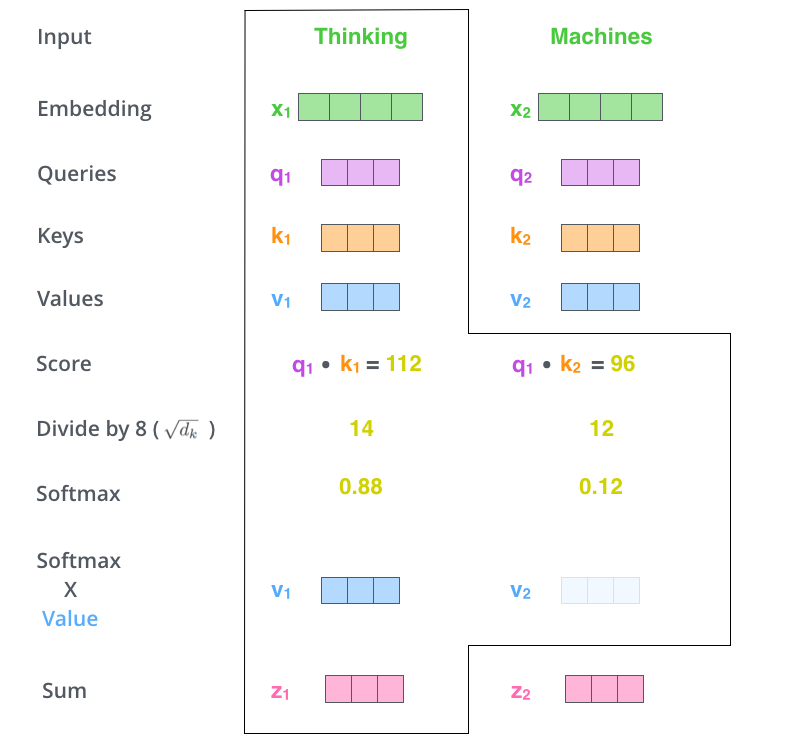
Self-Attention

• Have a collection of N objects (e.g. words in a sentence) represented as vectors
• Want to generate N representations of these objects that is context aware
  • Like an RNN (previous context) or bi-directional RNN (forwards and backwards context)
• For each object generate
  • A query: what this object is looking for in other objects
  • A key: what the object provides to other objects
  • A value: what the contribution of this object should be if key matches query
• Each of these is a different learned linear function (weight matrix + optional bias) of the input object

Self-Attention

http://jalammar.github.io/illustrated-transformer/

$$q_1 = 0001, q_2 = 1100$$ $$k_1 = 0010, k_2 = 0011$$ $$v_1 = 1010, v_2 = 0101$$

Replace norm/softmax with identity.

%%html
<div id="selfattn" style="width: 500px"></div>
<script>
    var divid = '#selfattn';
	jQuery(divid).asker({
	    id: divid,
	    question: "What is z1?",
		answers: ["0001","0101","0000","1010"],
        server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
		charter: chartmaker})
    
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();


</script>

Consider the two phrases:

"The cat breed"

"Breed the cat"

If we self-attend on these words, what is true about the outputs $z_1, z_2, z_3$ for the two phrases?

%%html
<div id="selfapos" style="width: 500px"></div>
<script>
    var divid = '#selfapos';
	jQuery(divid).asker({
	    id: divid,
	    question: "How to outputs differ?",
		answers: ["Completely different","Same but in different order","Identical"],
        server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
		charter: chartmaker})
    
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();


</script>

Positional Encoding

Neither the softmax nor addition operation cares about the order of words. Need to make the queries/keys/values position specific by adding a positional embedding to the input.

The positional encoding is a constant function of the sequence position ($pos$) and vector position ($i < k$). $$PE_{(pos,i)} = \left\{ \begin{array}{ll} sin\left(\frac{pos}{10000^\frac{i}{k}}\right) & i\; \mathrm{even} \\ cos\left(\frac{pos}{10000^\frac{i-1}{k}}\right) & i\; \mathrm{odd} \\ \end{array} \right. $$

# Code from https://www.tensorflow.org/tutorials/text/transformer
def get_angles(pos, i, d_model):
    angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
    return pos * angle_rates

def positional_encoding(position, d_model):
    angle_rads = get_angles(np.arange(position)[:, np.newaxis],
                          np.arange(d_model)[np.newaxis, :],
                          d_model)
    # apply sin to even indices in the array; 2i
    angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
    # apply cos to odd indices in the array; 2i+1
    angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])

    return angle_rads

import numpy as np, matplotlib.pyplot as plt
tokens = 10; dimensions = 64
pos_encoding = positional_encoding(tokens, dimensions)
plt.figure(figsize=(12,6)); plt.pcolormesh(pos_encoding, cmap='viridis')
plt.xlabel('Embedding Dimensions'); plt.xlim((0, dimensions)); plt.ylim((tokens,0))
plt.ylabel('Token Position'); plt.colorbar();plt.show()

Positional Encoding

First values of encoding cycle quickly, later positions more slowly.

p =  positional_encoding(20000,100)
plt.plot(p[:,50],label='i = 50')
plt.plot(p[:,-1],label='i = 99')
plt.xlabel('pos')
plt.legend();

Multi-headed Attention

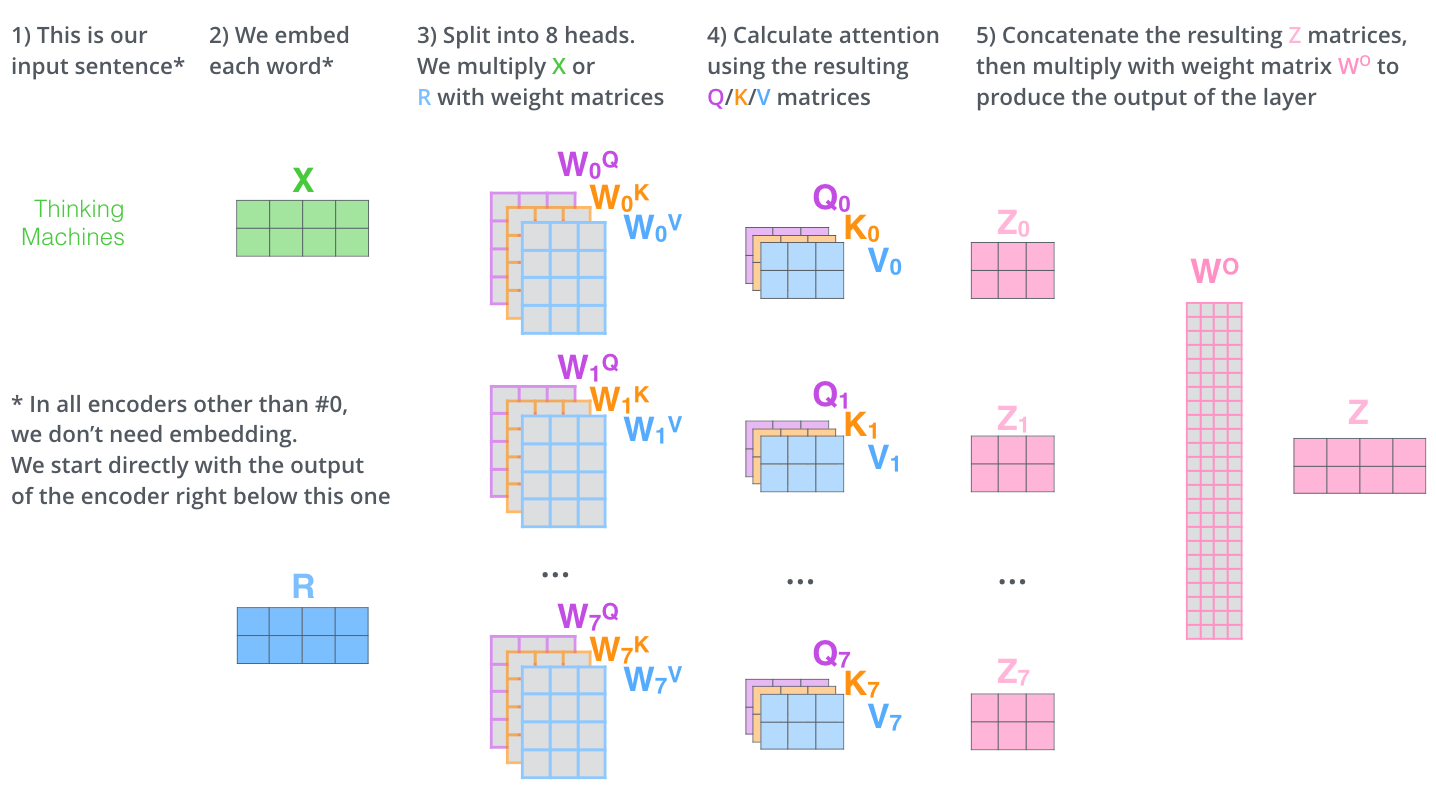
How does multi-headed attention differ from simply increasing the dimension of the query/key/value?

Transformers

Encoder

• Positional encoding on input
• Stack of self-attention + feed forward network layers
• Residual connections across layers
• Layer normalization

Decoder

• Input is its own output
• Positional encoding on input
• Self-attention to input
  • Masked: ignore what hasn't been output yet
• Not-self attention to input and encoder output
• Residual connections and layer normalization

%%html
<div id="transpar" style="width: 500px"></div>
<script>
    var divid = '#transpar';
	jQuery(divid).asker({
	    id: divid,
	    question: "What parts of the transformer can be parallelized across the input?",
		answers: ["E","D","E+D","None"],
        extra: ["Encoder only","Decoder only","Encoder and decoder","Neither encoder nor decoder"],
        server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
		charter: chartmaker})
    
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();


</script>

Universal Transformer

https://arxiv.org/pdf/1807.03819.pdf

https://ai.googleblog.com/2018/08/moving-beyond-translation-with.html

We've gone to all this trouble to eliminate recurrence so let's put it back!

Instead of recurring over the sequence we are recurring over applications of the transformer (the depth).

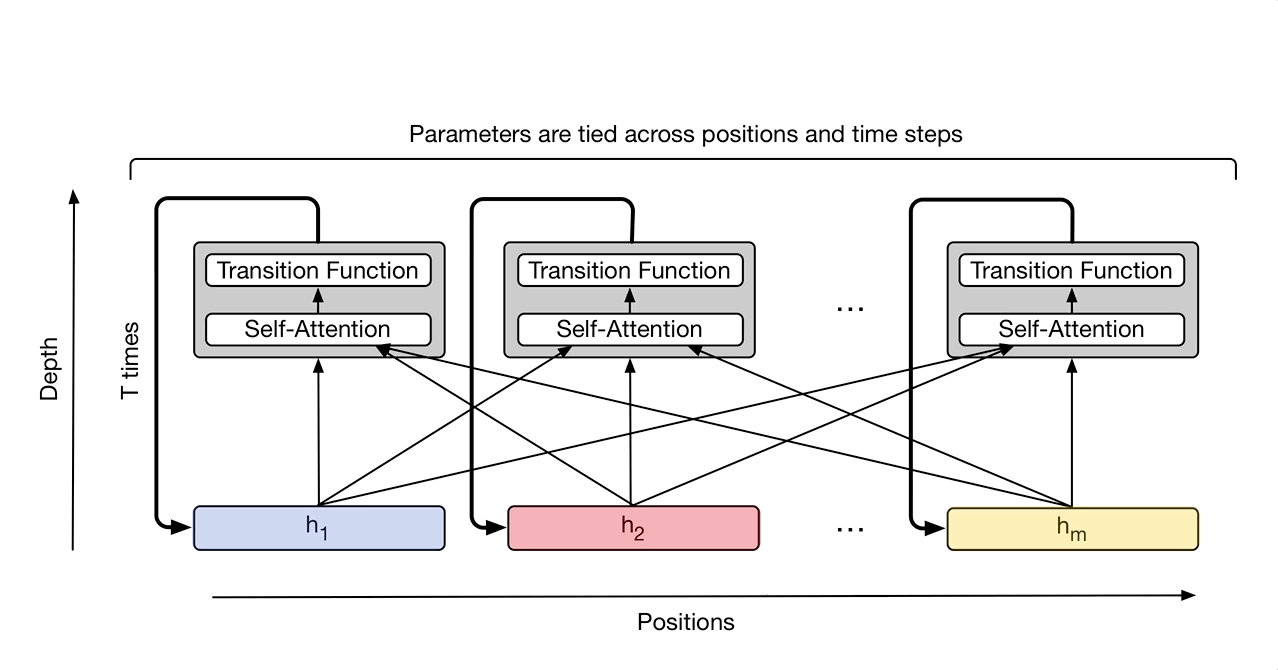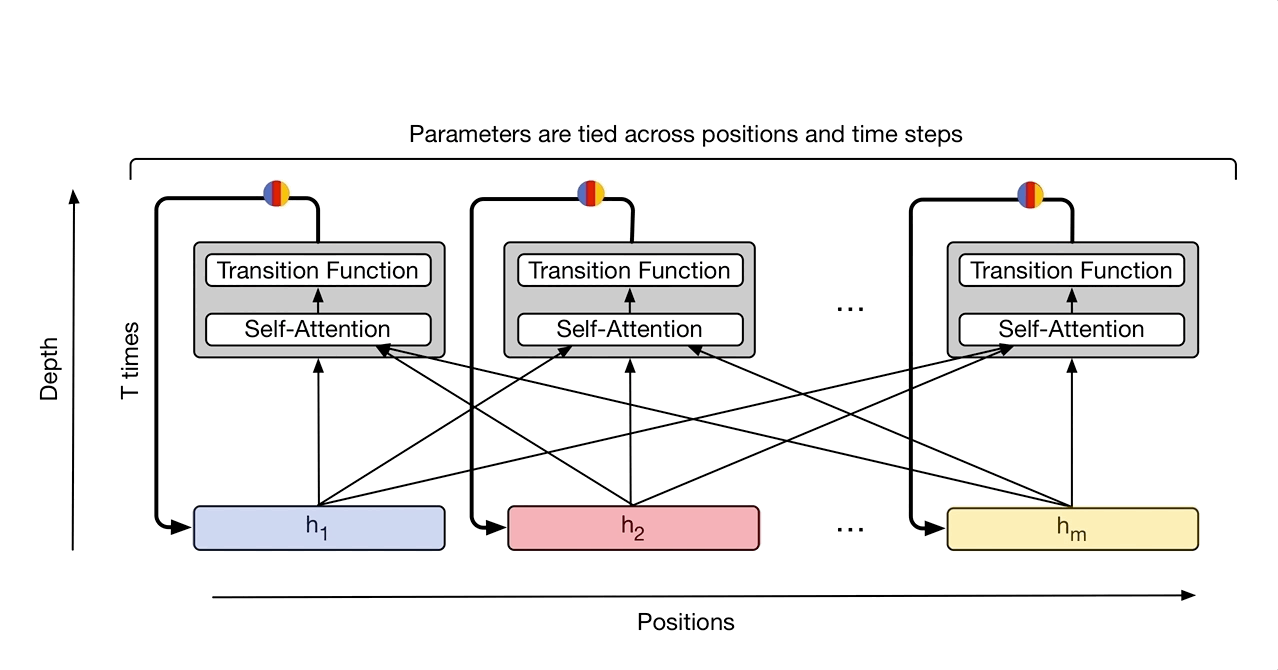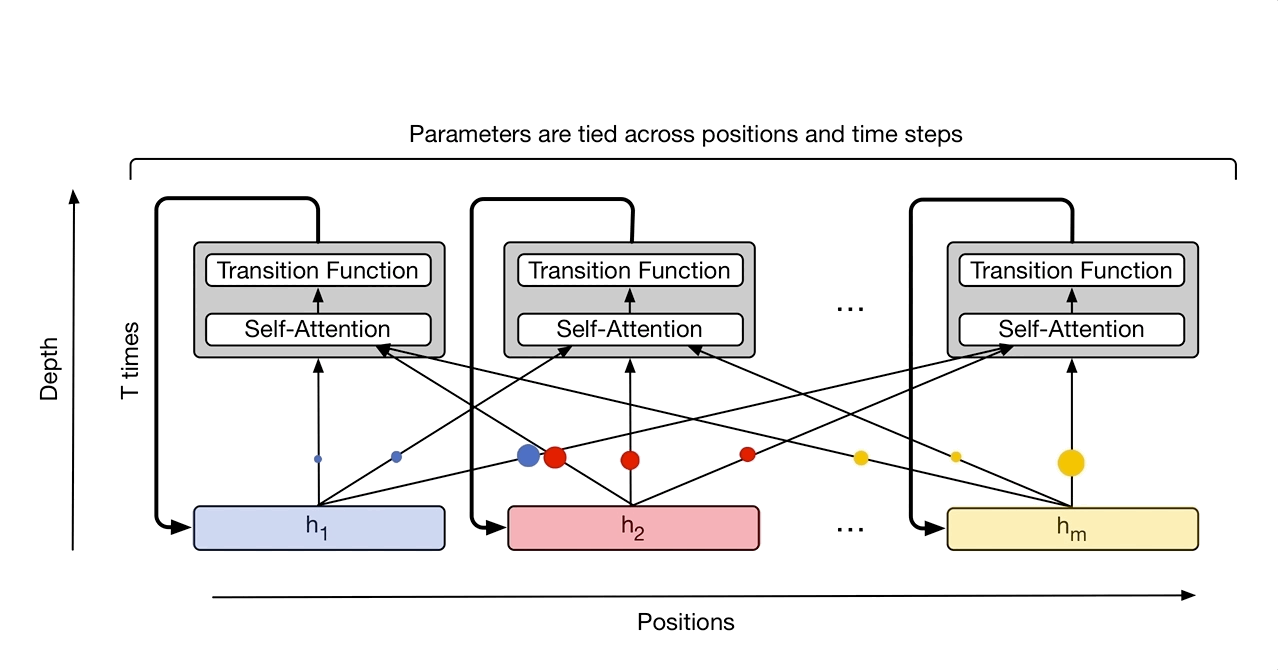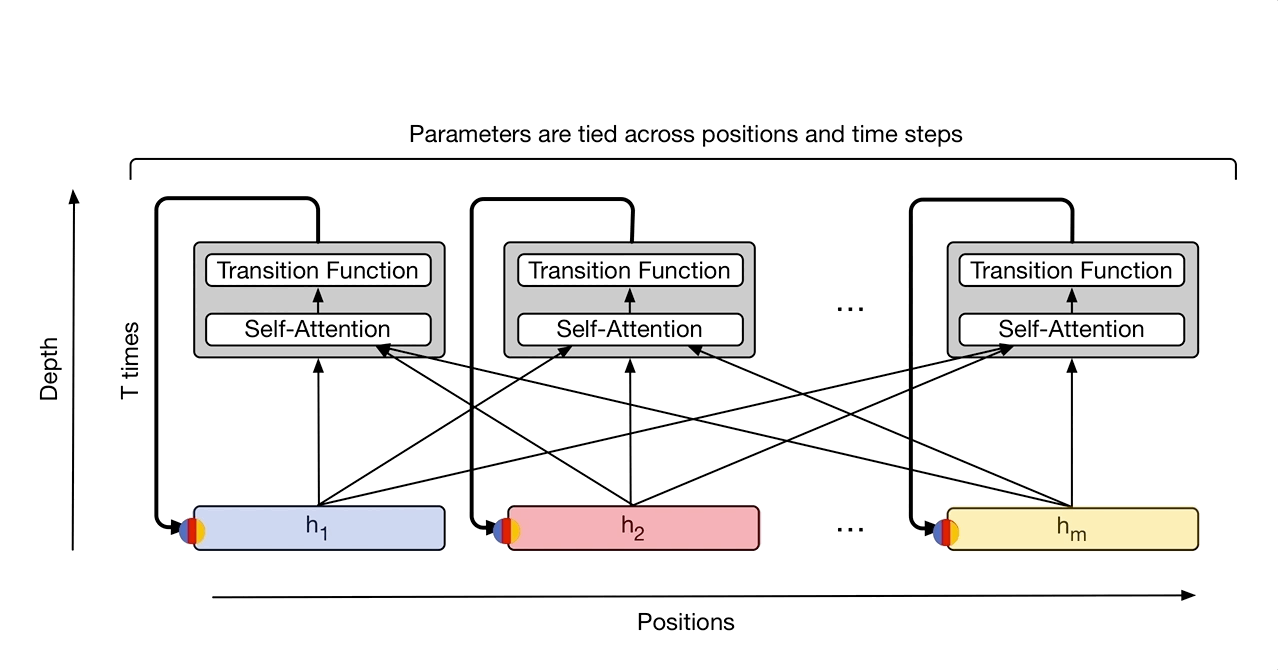
How is a universal transform that is applied 6 times different from a standard transformer with 6 layers?

Universal Transformer

A universal transformer supports dynamic halting. The number of iterations is decided by the output of the transformer.

Adaptive Computation Time: https://arxiv.org/abs/1603.08983

• Part of the output for each embedding is a halting probability (e.g. dense network applied to output embedding)
• Once this probability exceeds a threshold the embedding is no longer updated.

https://mostafadehghani.com/2019/05/05/universal-transformers/

Universal Transformer

• Encoder and decoder are separate recurrences

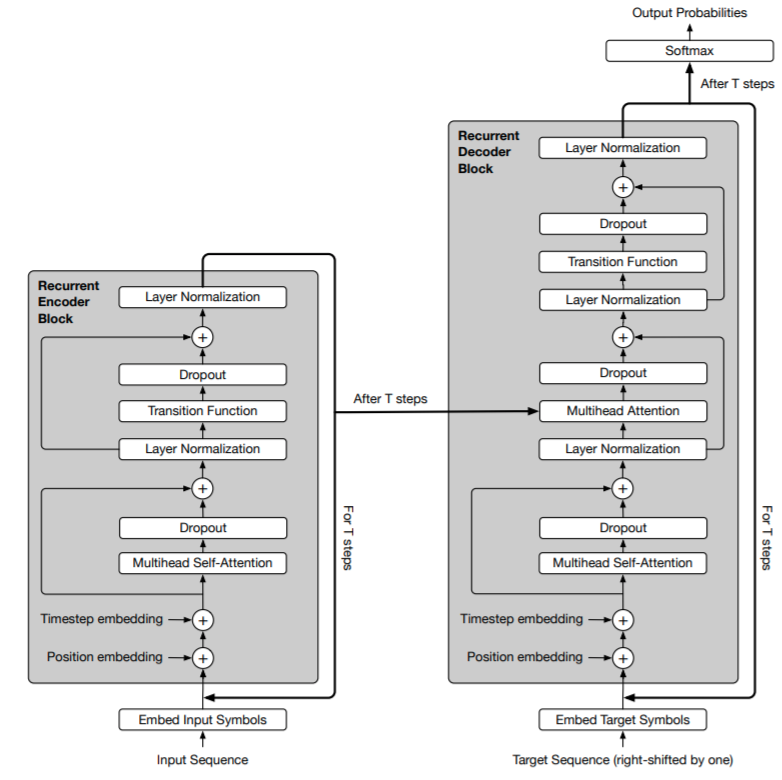
• Both position and timestep embeddings

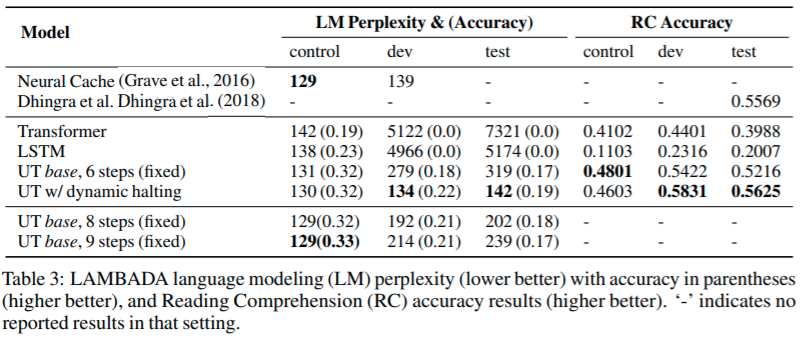
Average number of steps with dynamic halting was 8.2

%%html
<div id="univteach" style="width: 500px"></div>
<script>
    var divid = '#univteach';
	jQuery(divid).asker({
	    id: divid,
	    question: "Can a universal transformer be trained using teacher forcing?",
		answers: ["Yes","No","Maybe"],
        server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
		charter: chartmaker})
    
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();


</script>

Sparse Transformers

Don't attend to everything. https://arxiv.org/pdf/1904.10509.pdf

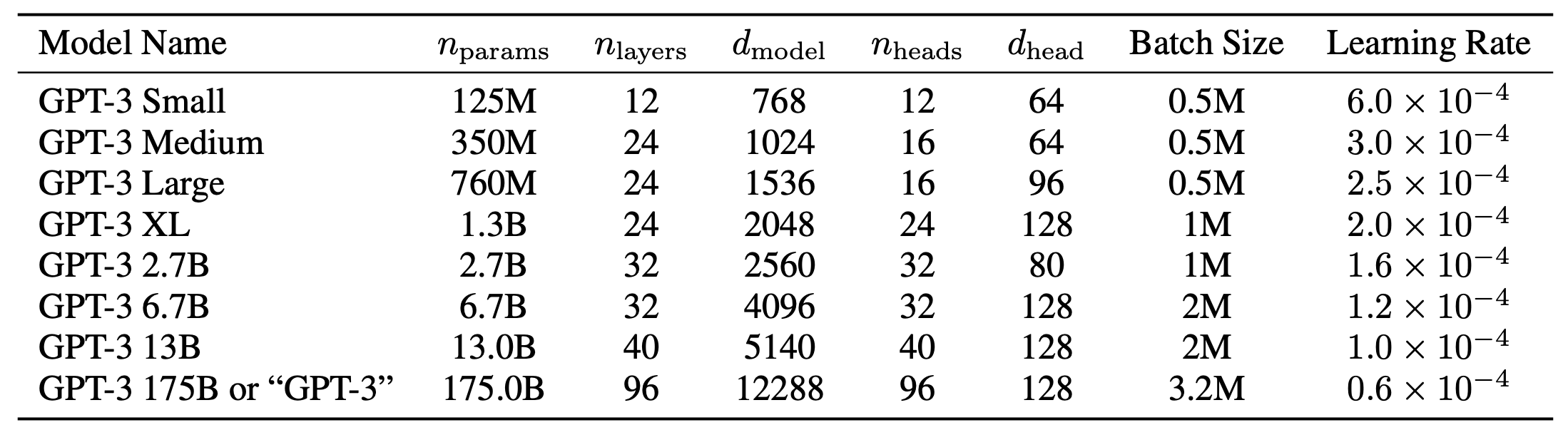
GPT-3: Generative pre-trained transformer

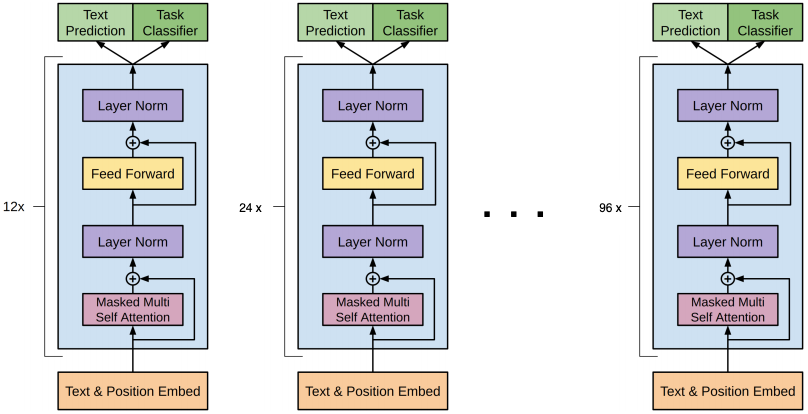
https://arxiv.org/pdf/2005.14165.pdf

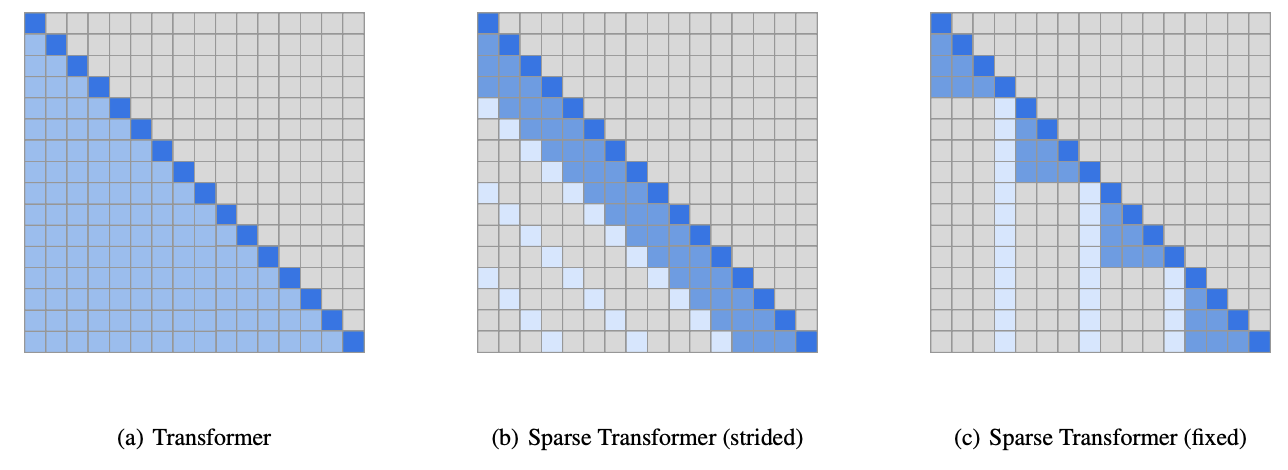
A decoder only transformer

• alternating dense and sparse attention patterns
• layer normalization
• really, really, really, really big

PyTorch Transformers

import torch
import torch.nn as nn
import torch.nn.functional as F

Like with with RNNs the first dimension is the sequence length and the second the batch (and there isn't an option to reverse it).

https://pytorch.org/docs/stable/generated/torch.nn.Transformer.html#torch.nn.Transformer

Why would we want to mask the input sequence?

Example

class SeqDataset(torch.utils.data.Dataset):
    def __init__(self, fname):
        #process whole file into memory
        self.seqs = []
        self.labels = []
        encodings = {'a': [1,0,0,0],'c': [0,1,0,0], 'g': [0,0,1,0], 't': [0,0,0,1], 'n': [0,0,0,0]}
        for line in open('train.B.txt'):
            seq,label = line.split()
            self.seqs.append(torch.tensor(list(map(lambda c: encodings[c], seq.lower())),dtype=torch.float32))
            self.labels.append(float(label))        
            
    #a mappable dataset needs __len__ and __getitem__
    def __len__(self):
        return len(self.seqs)
    def __getitem__(self, idx):
        return {'seq':self.seqs[idx], 'label': self.labels[idx]}

dataset = SeqDataset('train.B.txt')

Example

We need a custom collate_fn since the default will collate with the batch as the first dimension.

Fortunately, torch.nn.utils.rnn.pad_sequence does what we want (we don't need the padding).

def collate_seq(batch):
    return {
        'seq': torch.nn.utils.rnn.pad_sequence([ex['seq'] for ex in batch]), 
        'label': torch.tensor([ex['label'] for ex in batch])
    }

dataloader = torch.utils.data.DataLoader(dataset, batch_size=20, shuffle=True,collate_fn=collate_seq)

batch = next(iter(dataloader))
batch['seq'].shape

torch.Size([250, 20, 4])

batch['label'].shape

torch.Size([20])

Example

T = nn.TransformerEncoder(nn.TransformerEncoderLayer(d_model=4,nhead=4),num_layers=6)

/home/dkoes/.local/lib/python3.10/site-packages/torch/nn/modules/transformer.py:286: UserWarning: enable_nested_tensor is True, but self.use_nested_tensor is False because encoder_layer.self_attn.batch_first was not True(use batch_first for better inference performance)
  warnings.warn(f"enable_nested_tensor is True, but self.use_nested_tensor is False because {why_not_sparsity_fast_path}")

T.forward(batch['seq']).shape

torch.Size([250, 20, 4])

Model

class Model(nn.Module):
    def __init__(self,k,n):
        super(Model, self).__init__()

        # Default transformer
        self.T = nn.TransformerEncoder(nn.TransformerEncoderLayer(d_model=4,nhead=4),num_layers=6)
        # Fully connected layer
        self.fc = nn.Linear(k*n, 1)
    
    def forward(self, x):      
        batch_size = x.size(1)
        embedding = self.T(x)
        #swap batch an sequence dimensions
        x = x.permute(1,0,2).reshape(batch_size,-1)
        out = self.fc(x).flatten()
        
        return out

%%time
model = Model(k=4,n=250).to('cuda')
optimizer = torch.optim.Adam(model.parameters(), lr=0.0001)

losses = []
for i,batch in enumerate(dataloader):
    optimizer.zero_grad()
    output = model(batch['seq'].to('cuda'))
    labels = batch['label'].type(torch.float32).to('cuda')
    loss = F.mse_loss(output,labels)
    loss.backward()
    optimizer.step()
    losses.append(loss.item())

CPU times: user 2min 19s, sys: 1.44 s, total: 2min 20s
Wall time: 2min 23s

plt.plot(losses)

[<matplotlib.lines.Line2D at 0x7fdf108c5690>]

Test

testset = SeqDataset('test.B.labeled.txt')
testloader = torch.utils.data.DataLoader(testset, batch_size=20,collate_fn=collate_seq)

pred = []
true = []
with torch.no_grad():
    for batch in testloader:
        output = model(batch['seq'].to('cuda'))
        true += batch['label']
        pred += output.tolist()

np.corrcoef(pred,true)

array([[1.        , 0.51435422],
       [0.51435422, 1.        ]])

def count_parameters(model):
    return sum(p.numel() for p in model.parameters() if p.requires_grad)

count_parameters(model)

112193

Deep Assign5

Model	Parameters	Correlation	Train time (1 batch)
RNN	198,913	0.35	2m 56s
LSTM	268,545	0.23	4m 44s
Transformer	112,193	0.52	2m 30s

Summary

CNN

• Receptive field size of kernel; successive applications expand field incrementally
• Good for identifying spatial, local features and learning hierarchy of features

RNN

• Receptive field is what it has seen so far
  • But has trouble "remembering" what it has seen
  • LSTM is better at remembering

Attention

• Receptive field is entire input
• Needs positional encoding to be position-specific (spatially aware)