In [1]:
%%html
<script src="https://bits.csb.pitt.edu/preamble.js"></script>
The RTX 4090 GPU has 16,384 cores and 128 streaming multiprocessors. A CUDA kernel is launched using 64 blocks and and 1024 threads:
Add<<<64, 1024>>>(A, B, C)
In [44]:
%%html
<div id="cudaq" style="width: 500px"></div>
<script>
var divid = '#cudaq';
jQuery(divid).asker({
id: divid,
question: "At a given moment, how many threads of this kernel can be executing concurrently?",
answers: ["64","1024","8192","16384","65536"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Recall¶
Backpropagation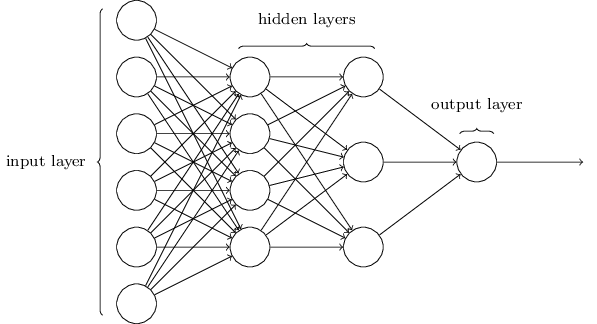 
- Feedforward.
$$a^{l} = \sigma(z^{l})$$
2. Compute output error
$$\delta^{N} = \nabla_a L \odot \sigma'(z^N)$$
3. Backpropagate the error
$$\delta^{l} = ((w^{l+1})^T \delta^{l+1}) \odot
\sigma'(z^{l})$$
4. Calculate gradients
$$\frac{\partial L}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \text{ and } \frac{\partial L}{\partial b^l_j} = \delta^l_j$$
Weight Initialization¶
What happens with back propagation if weights/biases are initialized to zero with ReLU? Sigmoid?
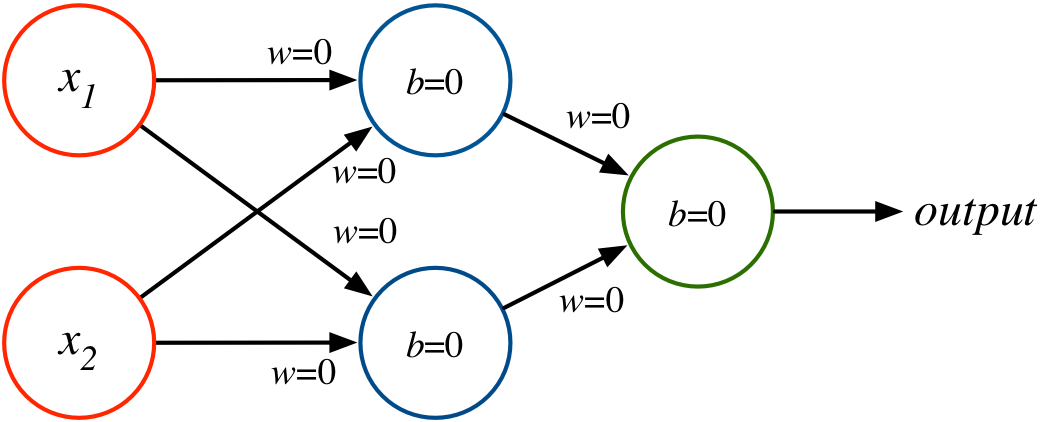
Weight Initialization¶
- constant - (e.g. all zero), almost never a good idea
- uniform - sample uniformly from range $(a,b)$, e.g. $(0,1)$
- positive unitball - sample from $(0,1)$ such that layer weights sum to 1
- Gaussian - sample from normal distribution
- Xavier - sample uniform distribution with range determined by fan-in/fan-out
- MSRA - sample normal distribution with variance determined by fan-in/fan-out
- https://arxiv.org/pdf/1502.01852.pdf
- compared to Xavier, works better with non-linear activation functions
Xavier Initialization¶
Sample from uniform distribution $(-a,a)$ where $$a = \sqrt{\frac{6}{\mathrm{fan}_\mathrm{in}+\mathrm{fan}_\mathrm{out}}}$$
The goal here is to maintain a constant variance both forwards and backwards.
Sometimes multiply by an activation function dependent scaling factor (gain).
Weight Initialization¶
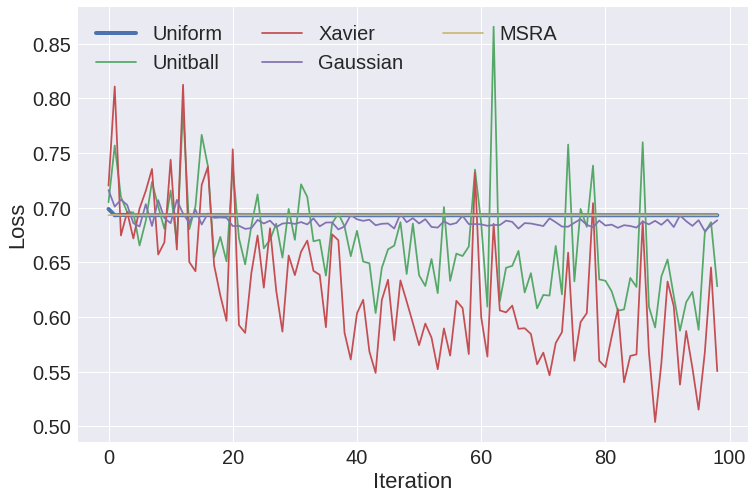
Weight Initialization¶
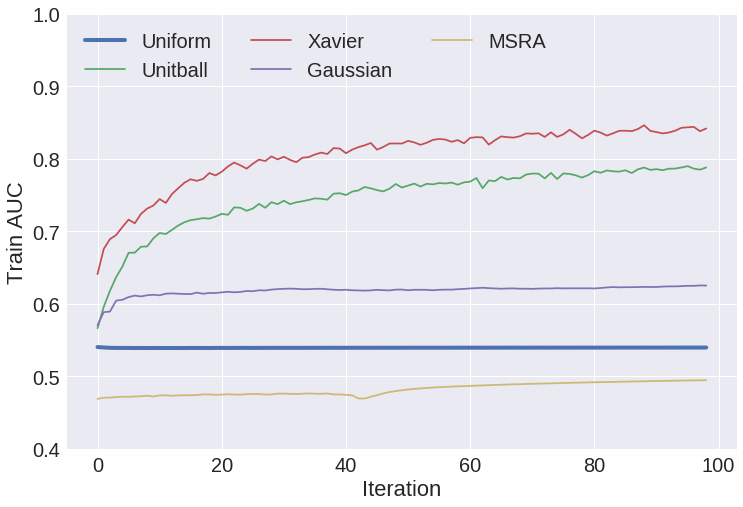
Weight Initialization¶
Deep Learning¶
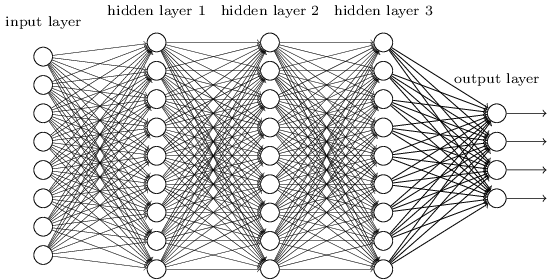
A deep network is not more powerful (recall can approximate any function with a single layer), but may be more concise - can approximate some functions with many fewer nodes.
In [45]:
%%html
<div id="deepq" style="width: 500px"></div>
<script>
var divid = '#deepq';
jQuery(divid).asker({
id: divid,
question: "Intuitively, which part of a deep network will learn faster?",
answers: ["Early layers","Later layers","Uniform"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Vanishing Gradients¶
Since weights tend to start out small and sigmoid derivatives are small, gradients tend to be smaller earlier in the network, resulting in slower learning (smaller weight updates).
However, if weights are large, the opposite can happen - the exploding gradient problem.
The unstable gradient problem means that layers tend to learn at different speeds.
In [46]:
%%html
<div id="vangrad" style="width: 500px"></div>
<script>
var divid = '#vangrad';
jQuery(divid).asker({
id: divid,
question: "Intuitively, which activation function is less likely to result in vanishing gradients?",
answers: ["Sigmoid","tanh","ReLU"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
ReLUs¶
ReLUs tend to result in faster training, but they can die.
LeakyReLU's are a proposed workaround.
Also, exponential linear units (ELUs) $$ y = \left\{ \begin{array}{lr} x & \mathrm{if} \; x > 0 \\ \alpha (e^x-1) & \mathrm{if} \; x \le 0 \end{array} \right. $$
In [7]:
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(x,np.maximum(0,x)+0.1*(np.exp(np.minimum(x,0))-1),linewidth=3,label="alpha = 0.1");
plt.plot(x,np.maximum(0,x)+(np.exp(np.minimum(x,0))-1),linewidth=1,label="alpha = 1.0");
plt.legend(loc='best');
Convolution Filters¶
A filter applies a convolution kernel to an image.
The kernel is represented by an $n$x$n$ matrix where the target pixel is in the center.
The output of the filter is the sum of the products of the matrix elements with the corresponding pixels.
Examples (from Wikipedia:
 |
|
|
| Identity | Blur | Edge Detection |
Edges¶
In [8]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib import cm
In [9]:
from PIL import Image, ImageFilter
dog = Image.open('figs/dog.png')
f = plt.figure(figsize=(12,6))
f.add_subplot(1, 2, 1)
plt.imshow(np.array(dog),cmap = cm.Greys_r)
f.add_subplot(1, 2, 2)
plt.imshow(np.array(dog.filter(ImageFilter.FIND_EDGES)), cmap=cm.Greys_r)
print(ImageFilter.FIND_EDGES.filterargs)
((3, 3), 1, 0, (-1, -1, -1, -1, 8, -1, -1, -1, -1))
Edges¶
What would these convolutions do?
In [10]:
v = np.array([
[-1,0,1],
[-1,0,1],
[-1,0,1]])
h = np.array([
[-1,-1,-1],
[0,0,0],
[1,1,1]])
In [11]:
f = plt.figure(figsize=(12,6))
f.add_subplot(1, 2, 1)
plt.imshow(np.array(dog.filter(ImageFilter.Kernel((3,3),v.flatten(),1))), cmap=cm.Greys_r)
f.add_subplot(1, 2, 2)
plt.imshow(np.array(dog.filter(ImageFilter.Kernel((3,3),h.flatten(),1))), cmap=cm.Greys_r);
Feature Maps¶
We can think of a kernel as identifying a feature in an image and the resulting image as a feature map that has high values (white) where the feature is present and low values (black) elsewhere.
Feature maps retain the spatial relationship* between features present in the original image.*
Each feature map is called a channel. For color images, the input starts with 3 channels. Successive layers will have an output channel for each kernel.
Convolutional Layers¶
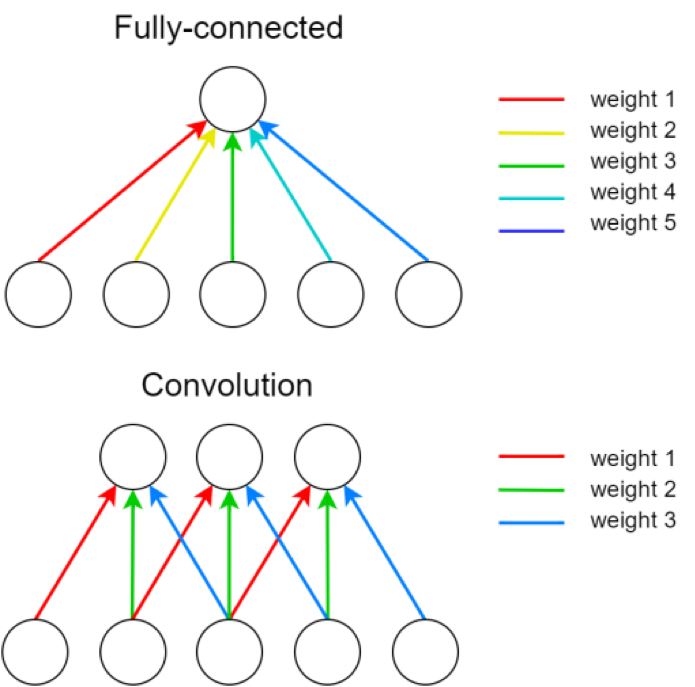A single kernel is applied across the input. For each output feature map there is a single set of weights.
Convolutional Layers¶
For images, each pixel is an input feature. Each hidden layer is a set of feature maps.
Consider an input image with 100 pixels. In a classic neural network, we hook these pixels up to a hidden layer with 10 nodes. In a CNN, we hook these pixels up to a convolutional layer with a 3x3 kernel and 10 output feature maps.
In [12]:
%%html
<div id="weightcnt" style="width: 500px"></div>
<script>
var divid = '#weightcnt';
jQuery(divid).asker({
id: divid,
question: "Which network has more parameters to learn?",
answers: ["Classic","CNN"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
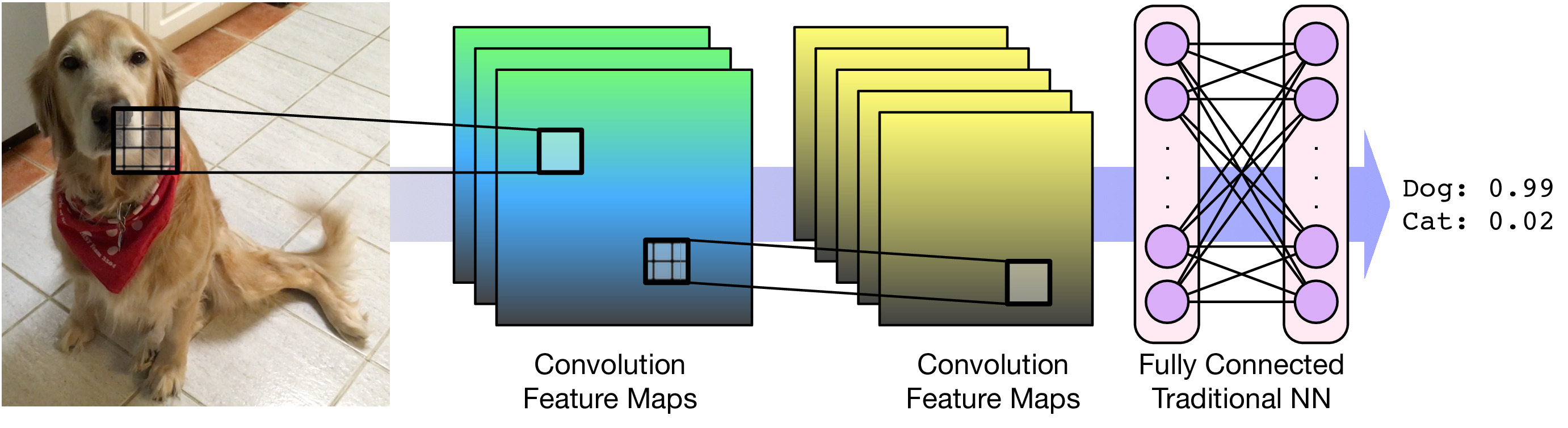
Convolution Parameters¶
- kernel_size size of kernel
- stride how much to shift kernel
- padding amount of implicit padding at edges (usually zero, but can extend/reflect/wrap values)
- dilation the spacing between the kernel points
- groups how inputs connect to outputs - default is all inputs (channels) effect all outputs. That is, your kernel has C x W x H weights.
https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md
We apply a convolution with kernel_size 5, stride 3, and padding 0 to a 20x20 image
In [13]:
%%html
<div id="stridecnn" style="width: 500px"></div>
<script>
var divid = '#stridecnn';
jQuery(divid).asker({
id: divid,
question: "What will be the size of the output?",
answers: ["6x6","5x5","20x20","17x17","7x7"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Pooling¶
Pooling layers apply a fixed convolution (usually the non-linear MAX kernel). The kernel is usually applied with a stride to reduce the size of the layer.
- faster to train
- fewer parameters to fit
- less sensitive to small changes (MAX)
Deep Learning Frameworks¶
Three different approaches to defining a network.
- Declarative Describe the network using some custom format.
- Programmatic Static Graph Creation Build the network using code.
- Programmatic Dynamic Graph Creation The network is built as you perform its constitutive operations
Declarative Example: Caffe¶
layer {
name: "unit1_pool"
type: "Pooling"
bottom: "data"
top: "unit1_pool"
pooling_param {
pool: AVE
kernel_size: 2
stride: 2
}
}
layer {
name: "unit1_conv"
type: "Convolution"
bottom: "unit1_pool"
top: "unit1_conv"
convolution_param {
num_output: 32
pad: 1
kernel_size: 3
stride: 1
weight_filler {
type: "xavier"
symmetric_fraction: 1.0
}
}
}
Static Graph Example: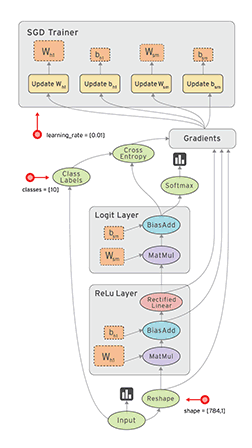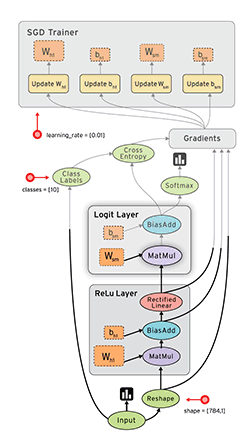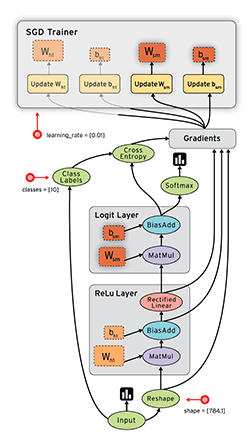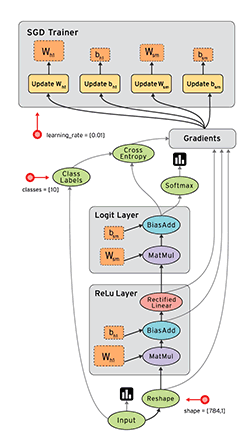 
TensorFlow 1.0
TensorFlow is Google's open-source library for computation on dataflow graphs.
Data is represented as tensors, multi-dimensional blocks of data.
Each node in the dataflow graph is executed on a single resource (e.g. CPU or GPU).
Nodes are executed as data becomes available.
This is a very generic, low-level library.
Building the Graph¶
The first step of using TensorFlow is building the dataflow graph. This is done programmatically in Python.
Placeholders are inputs into the dataflow graph and must be declared as such.
Each function returns a graph node - it does not actually perform the operation.
Note: Placeholders are gone in Tensorflow 2.0, which follows an eager execution model (dynamic graph creation).
In [ ]:
x = tf.placeholder(tf.float32, shape=[None, 28, 28, 1])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
def weight_variable(shape): #randomly sample weights
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape): # start with positive offset for ReLUs
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1) # apply ReLU activation function to conv
h_pool1 = max_pool_2x2(h_conv1)
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1, W_fc2) + b_fc2
#loss
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y_conv, labels=y_))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
#initialize session
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
#run a single iteration of training
_, loss = sess.run([train_step, cross_entropy],feed_dict={x: IMAGES, y_: LABELS})
PyTorch Tensors¶
Tensor is very similar to numpy.array in functionality.
- Is allocated to a device (CPU vs GPU)
- Potentially maintains autograd information
In [14]:
import torch # note package is not called pytorch
T = torch.rand(3,4)
T
Out[14]:
tensor([[0.7155, 0.1139, 0.2413, 0.2633],
[0.1385, 0.7052, 0.5210, 0.4216],
[0.5301, 0.8222, 0.8871, 0.5029]])
In [15]:
T.shape,T.dtype,T.device,T.requires_grad
Out[15]:
(torch.Size([3, 4]), torch.float32, device(type='cpu'), False)
Tensors on GPU¶
In [16]:
T = torch.rand(100000000)
In [17]:
%timeit T.dot(T)
14.9 ms ± 1.35 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
In [18]:
T = T.to('cuda')
T.device
--------------------------------------------------------------------------- AssertionError Traceback (most recent call last) /var/folders/c_/pwm7n7_174724g8zkkqlpr3m0000gn/T/ipykernel_40856/1449615246.py in <module> ----> 1 T = T.to('cuda') 2 T.device ~/Library/Python/3.9/lib/python/site-packages/torch/cuda/__init__.py in _lazy_init() 206 "multiprocessing, you must use the 'spawn' start method") 207 if not hasattr(torch._C, '_cuda_getDeviceCount'): --> 208 raise AssertionError("Torch not compiled with CUDA enabled") 209 if _cudart is None: 210 raise AssertionError( AssertionError: Torch not compiled with CUDA enabled
In [19]:
%timeit T.dot(T)
14.5 ms ± 1.57 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
numpy conversion¶
In [20]:
T.numpy()
Out[20]:
array([0.7513881 , 0.6466379 , 0.41595292, ..., 0.78812236, 0.40659142,
0.9700796 ], dtype=float32)
In [21]:
T.cpu().numpy()
Out[21]:
array([0.7513881 , 0.6466379 , 0.41595292, ..., 0.78812236, 0.40659142,
0.9700796 ], dtype=float32)
In [22]:
torch.from_numpy(np.array([1,3,4]))
Out[22]:
tensor([1, 3, 4])
Autograd¶
If any tensor of an operation requires_grad then the computation graph is stored along with any information needed for computing the gradient.
In [23]:
x = torch.tensor([3.0],requires_grad=True)
poly = x**3 + 4*x**2 + 2*x + 6 # poly' = 3x^2 + 8x + 2
In [24]:
poly
Out[24]:
tensor([75.], grad_fn=<AddBackward0>)
In [25]:
x.grad #no gradient computed yet
In [26]:
poly.backward()
In [27]:
x.grad
Out[27]:
tensor([53.])
In [28]:
3*(3.0)**2+8*(3.0)+2 # poly'(3.0)
Out[28]:
53.0
In [29]:
import torchviz
torchviz.make_dot(poly)
--------------------------------------------------------------------------- ModuleNotFoundError Traceback (most recent call last) /var/folders/c_/pwm7n7_174724g8zkkqlpr3m0000gn/T/ipykernel_40856/1072983260.py in <module> ----> 1 import torchviz 2 3 torchviz.make_dot(poly) ModuleNotFoundError: No module named 'torchviz'
What information does each node need to store in order to compute grad?
Important¶
Not calling backward on chains of gradient-retaining computations will use more and more memory.
In [30]:
T = torch.tensor([1,2,3],dtype=torch.float,requires_grad=True)
for _ in range(100):
T = T + torch.rand_like(T)
In [31]:
g = T.grad_fn
while g.next_functions:
print(g)
g = g.next_functions[0][0]
<AddBackward0 object at 0x127d5ddf0> <AddBackward0 object at 0x127aaf370> <AddBackward0 object at 0x127d5dd90> <AddBackward0 object at 0x127d5d9a0> <AddBackward0 object at 0x127d346d0> <AddBackward0 object at 0x127ba4550> <AddBackward0 object at 0x1473a6f70> <AddBackward0 object at 0x1473a6fd0> <AddBackward0 object at 0x1474140d0> <AddBackward0 object at 0x147414190> <AddBackward0 object at 0x147414250> <AddBackward0 object at 0x147414310> <AddBackward0 object at 0x1474143d0> <AddBackward0 object at 0x147414490> <AddBackward0 object at 0x147414550> <AddBackward0 object at 0x147414610> <AddBackward0 object at 0x1474146d0> <AddBackward0 object at 0x147414790> <AddBackward0 object at 0x127cf34f0> <AddBackward0 object at 0x127c7e580> <AddBackward0 object at 0x147414850> <AddBackward0 object at 0x147414910> <AddBackward0 object at 0x1474149d0> <AddBackward0 object at 0x147414a90> <AddBackward0 object at 0x147414b50> <AddBackward0 object at 0x147414c10> <AddBackward0 object at 0x147414cd0> <AddBackward0 object at 0x147414d90> <AddBackward0 object at 0x147414e50> <AddBackward0 object at 0x147414f10> <AddBackward0 object at 0x147414fd0> <AddBackward0 object at 0x1474170d0> <AddBackward0 object at 0x147417190> <AddBackward0 object at 0x147417250> <AddBackward0 object at 0x147417310> <AddBackward0 object at 0x1474173d0> <AddBackward0 object at 0x147417490> <AddBackward0 object at 0x147417550> <AddBackward0 object at 0x147417610> <AddBackward0 object at 0x1474176d0> <AddBackward0 object at 0x147417790> <AddBackward0 object at 0x147417850> <AddBackward0 object at 0x147417910> <AddBackward0 object at 0x1474179d0> <AddBackward0 object at 0x147417a90> <AddBackward0 object at 0x147417b50> <AddBackward0 object at 0x147417c10> <AddBackward0 object at 0x147417cd0> <AddBackward0 object at 0x147417d90> <AddBackward0 object at 0x147417e50> <AddBackward0 object at 0x147417f10> <AddBackward0 object at 0x147417fd0> <AddBackward0 object at 0x14741b0d0> <AddBackward0 object at 0x14741b190> <AddBackward0 object at 0x14741b250> <AddBackward0 object at 0x14741b310> <AddBackward0 object at 0x14741b3d0> <AddBackward0 object at 0x14741b490> <AddBackward0 object at 0x14741b550> <AddBackward0 object at 0x14741b610> <AddBackward0 object at 0x14741b6d0> <AddBackward0 object at 0x14741b7c0> <AddBackward0 object at 0x14741b880> <AddBackward0 object at 0x14741b940> <AddBackward0 object at 0x14741ba00> <AddBackward0 object at 0x14741bac0> <AddBackward0 object at 0x14741bb80> <AddBackward0 object at 0x14741bc40> <AddBackward0 object at 0x14741bd00> <AddBackward0 object at 0x14741bdc0> <AddBackward0 object at 0x14741be80> <AddBackward0 object at 0x14741bf40> <AddBackward0 object at 0x14741e040> <AddBackward0 object at 0x14741e100> <AddBackward0 object at 0x14741e1c0> <AddBackward0 object at 0x14741e280> <AddBackward0 object at 0x14741e340> <AddBackward0 object at 0x14741e400> <AddBackward0 object at 0x14741e4c0> <AddBackward0 object at 0x14741be80> <AddBackward0 object at 0x14741beb0> <AddBackward0 object at 0x14741bdf0> <AddBackward0 object at 0x14741bd30> <AddBackward0 object at 0x14741bc70> <AddBackward0 object at 0x14741bbb0> <AddBackward0 object at 0x14741baf0> <AddBackward0 object at 0x14741ba30> <AddBackward0 object at 0x14741b970> <AddBackward0 object at 0x14741b8b0> <AddBackward0 object at 0x14741b7f0> <AddBackward0 object at 0x14741b700> <AddBackward0 object at 0x14741b640> <AddBackward0 object at 0x14741b580> <AddBackward0 object at 0x14741b4c0> <AddBackward0 object at 0x14741b400> <AddBackward0 object at 0x14741b340> <AddBackward0 object at 0x14741b280> <AddBackward0 object at 0x14741b1c0> <AddBackward0 object at 0x14741b070> <AddBackward0 object at 0x127cf34f0>
What happens when I call backward on T?
In [32]:
T.backward()
--------------------------------------------------------------------------- RuntimeError Traceback (most recent call last) /var/folders/c_/pwm7n7_174724g8zkkqlpr3m0000gn/T/ipykernel_40856/145981819.py in <module> ----> 1 T.backward() ~/Library/Python/3.9/lib/python/site-packages/torch/_tensor.py in backward(self, gradient, retain_graph, create_graph, inputs) 305 create_graph=create_graph, 306 inputs=inputs) --> 307 torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs) 308 309 def register_hook(self, hook): ~/Library/Python/3.9/lib/python/site-packages/torch/autograd/__init__.py in backward(tensors, grad_tensors, retain_graph, create_graph, grad_variables, inputs) 148 149 grad_tensors_ = _tensor_or_tensors_to_tuple(grad_tensors, len(tensors)) --> 150 grad_tensors_ = _make_grads(tensors, grad_tensors_) 151 if retain_graph is None: 152 retain_graph = create_graph ~/Library/Python/3.9/lib/python/site-packages/torch/autograd/__init__.py in _make_grads(outputs, grads) 49 if out.requires_grad: 50 if out.numel() != 1: ---> 51 raise RuntimeError("grad can be implicitly created only for scalar outputs") 52 new_grads.append(torch.ones_like(out, memory_format=torch.preserve_format)) 53 else: RuntimeError: grad can be implicitly created only for scalar outputs
In [33]:
T.backward(gradient=torch.zeros_like(T))
Modules vs Functional¶
Modules are objects that can be initialized with default parameters and store any learnable parameters. Learnable parameters can be easily extracted from the module (and any member modules). Modules are called as functions on their inputs.
Functional APIs maintain no state. All parameters are passed when the function is called.
In [34]:
import torch.nn as nn
import torch.nn.functional as F
In [35]:
T = torch.tensor([1,2,3],dtype=torch.float32)
fc = nn.Linear(3,1) # module implementation of fully connected layer
fc(T) # output REQURES_GRAD because learnable parameters require grad
Out[35]:
tensor([-0.1171], grad_fn=<AddBackward0>)
In [36]:
fc._parameters
Out[36]:
OrderedDict([('weight',
Parameter containing:
tensor([[-0.0152, -0.2419, 0.3170]], requires_grad=True)),
('bias',
Parameter containing:
tensor([-0.5690], requires_grad=True))])
In [37]:
weights = torch.rand((1,3)) # no bias
F.linear(T,weights) #no tensors require_grad, so neither does output
Out[37]:
tensor([0.7049])
A network is a module¶
To define a network we create a module with submodules for operations with learnable parameters. Generally use functional API for operations without learnable parameters.
In [39]:
class MyNet(nn.Module):
def __init__(self): #initialize submodules here - this defines our network architecture
super(MyNet, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, stride=1)
self.fc1 = nn.Linear(X, 10) #mystery X
def forward(self, x): # this actually applies the operations
x = self.conv1(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = torch.flatten(x, 1)
x = self.fc1(x)
return x
In [40]:
%%html
<div id="fcques" style="width: 500px"></div>
<script>
var divid = '#fcques';
jQuery(divid).asker({
id: divid,
question: "If the input is a 28x28 single-channel image, what does X have to be?",
answers: ["280","50,176","2304","43,264","3136"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Dimensions¶
All operations assume inputs come in batches of examples.
In [41]:
C = nn.Conv2d(in_channels=1,out_channels=1,kernel_size=3,padding=1)
C(torch.rand((1,10,10)))
--------------------------------------------------------------------------- RuntimeError Traceback (most recent call last) /var/folders/c_/pwm7n7_174724g8zkkqlpr3m0000gn/T/ipykernel_40856/2410665575.py in <module> 1 C = nn.Conv2d(in_channels=1,out_channels=1,kernel_size=3,padding=1) ----> 2 C(torch.rand((1,10,10))) ~/Library/Python/3.9/lib/python/site-packages/torch/nn/modules/module.py in _call_impl(self, *input, **kwargs) 1100 if not (self._backward_hooks or self._forward_hooks or self._forward_pre_hooks or _global_backward_hooks 1101 or _global_forward_hooks or _global_forward_pre_hooks): -> 1102 return forward_call(*input, **kwargs) 1103 # Do not call functions when jit is used 1104 full_backward_hooks, non_full_backward_hooks = [], [] ~/Library/Python/3.9/lib/python/site-packages/torch/nn/modules/conv.py in forward(self, input) 444 445 def forward(self, input: Tensor) -> Tensor: --> 446 return self._conv_forward(input, self.weight, self.bias) 447 448 class Conv3d(_ConvNd): ~/Library/Python/3.9/lib/python/site-packages/torch/nn/modules/conv.py in _conv_forward(self, input, weight, bias) 440 weight, bias, self.stride, 441 _pair(0), self.dilation, self.groups) --> 442 return F.conv2d(input, weight, bias, self.stride, 443 self.padding, self.dilation, self.groups) 444 RuntimeError: Expected 4-dimensional input for 4-dimensional weight [1, 1, 3, 3], but got 3-dimensional input of size [1, 10, 10] instead
MNIST¶
In [42]:
from torchvision import datasets
train_data = datasets.MNIST(root='../data', train=True,download=True)
test_data = datasets.MNIST(root='../data', train=False,download=True)
/Users/dkoes/Library/Python/3.9/lib/python/site-packages/torchvision/io/image.py:11: UserWarning: Failed to load image Python extension: dlopen(/Users/dkoes/Library/Python/3.9/lib/python/site-packages/torchvision/image.so, 0x0006): Library not loaded: @rpath/libpng16.16.dylib
Referenced from: <5F6B6919-410D-397C-98F2-12C5934F9DBE> /Users/dkoes/Library/Python/3.9/lib/python/site-packages/torchvision/image.so
Reason: tried: '/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/System/Volumes/Preboot/Cryptexes/OS/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/System/Volumes/Preboot/Cryptexes/OS/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/System/Volumes/Preboot/Cryptexes/OS/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/System/Volumes/Preboot/Cryptexes/OS/Users/malfet/miniforge3/envs/py_39_torch-1.10.2/lib/libpng16.16.dylib' (no such file), '/usr/local/lib/libpng16.16.dylib' (no such file), '/usr/lib/libpng16.16.dylib' (no such file, not in dyld cache)
warn(f"Failed to load image Python extension: {e}")
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to ../data/MNIST/raw/train-images-idx3-ubyte.gz
0%| | 0/9912422 [00:00<?, ?it/s]
Extracting ../data/MNIST/raw/train-images-idx3-ubyte.gz to ../data/MNIST/raw Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to ../data/MNIST/raw/train-labels-idx1-ubyte.gz
0%| | 0/28881 [00:00<?, ?it/s]
Extracting ../data/MNIST/raw/train-labels-idx1-ubyte.gz to ../data/MNIST/raw Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to ../data/MNIST/raw/t10k-images-idx3-ubyte.gz
0%| | 0/1648877 [00:00<?, ?it/s]
Extracting ../data/MNIST/raw/t10k-images-idx3-ubyte.gz to ../data/MNIST/raw Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to ../data/MNIST/raw/t10k-labels-idx1-ubyte.gz
0%| | 0/4542 [00:00<?, ?it/s]
Extracting ../data/MNIST/raw/t10k-labels-idx1-ubyte.gz to ../data/MNIST/raw
In [150]:
train_data[0]
Out[150]:
(<PIL.Image.Image image mode=L size=28x28 at 0x7F20A4609FF0>, 5)
In [151]:
train_data[0][0]
Out[151]:
Inputs need to be tensors...
In [152]:
from torchvision import transforms
train_data = datasets.MNIST(root='../data', train=True,transform=transforms.ToTensor())
test_data = datasets.MNIST(root='../data', train=False,transform=transforms.ToTensor())
In [153]:
train_data[0][0]
Out[153]:
tensor([[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0118, 0.0706, 0.0706, 0.0706,
0.4941, 0.5333, 0.6863, 0.1020, 0.6510, 1.0000, 0.9686, 0.4980,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.1176, 0.1412, 0.3686, 0.6039, 0.6667, 0.9922, 0.9922, 0.9922,
0.9922, 0.9922, 0.8824, 0.6745, 0.9922, 0.9490, 0.7647, 0.2510,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1922,
0.9333, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922,
0.9922, 0.9843, 0.3647, 0.3216, 0.3216, 0.2196, 0.1529, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0706,
0.8588, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922, 0.7765, 0.7137,
0.9686, 0.9451, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.3137, 0.6118, 0.4196, 0.9922, 0.9922, 0.8039, 0.0431, 0.0000,
0.1686, 0.6039, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0549, 0.0039, 0.6039, 0.9922, 0.3529, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.5451, 0.9922, 0.7451, 0.0078, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0431, 0.7451, 0.9922, 0.2745, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.1373, 0.9451, 0.8824, 0.6275,
0.4235, 0.0039, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.3176, 0.9412, 0.9922,
0.9922, 0.4667, 0.0980, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1765, 0.7294,
0.9922, 0.9922, 0.5882, 0.1059, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0627,
0.3647, 0.9882, 0.9922, 0.7333, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.9765, 0.9922, 0.9765, 0.2510, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1804, 0.5098,
0.7176, 0.9922, 0.9922, 0.8118, 0.0078, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.1529, 0.5804, 0.8980, 0.9922,
0.9922, 0.9922, 0.9804, 0.7137, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0941, 0.4471, 0.8667, 0.9922, 0.9922, 0.9922,
0.9922, 0.7882, 0.3059, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0902, 0.2588, 0.8353, 0.9922, 0.9922, 0.9922, 0.9922, 0.7765,
0.3176, 0.0078, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0706, 0.6706,
0.8588, 0.9922, 0.9922, 0.9922, 0.9922, 0.7647, 0.3137, 0.0353,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.2157, 0.6745, 0.8863, 0.9922,
0.9922, 0.9922, 0.9922, 0.9569, 0.5216, 0.0431, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.5333, 0.9922, 0.9922, 0.9922,
0.8314, 0.5294, 0.5176, 0.0627, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000]]])
In [154]:
plt.imshow(train_data[0][0][0])
Out[154]:
<matplotlib.image.AxesImage at 0x7f1fb1a98f70>
Training MNIST¶
In [171]:
#process 10 randomly sampled images at a time
train_loader = torch.utils.data.DataLoader(train_data,batch_size=10,shuffle=True)
test_loader = torch.utils.data.DataLoader(test_data,batch_size=10,shuffle=False)
#instantiate our neural network and put it on the GPU
model = MyNet().to('cuda')
In [172]:
batch = next(iter(train_loader))
batch
Out[172]:
[tensor([[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
...,
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]]]),
tensor([5, 0, 3, 7, 5, 5, 2, 7, 9, 1])]
In [173]:
output = model(batch[0].to('cuda')) # model is on GPU, so must put input there too
output
Out[173]:
tensor([[-0.0448, 0.0352, -0.1200, -0.0358, 0.0289, 0.0598, -0.1537, -0.0834,
0.0161, -0.0253],
[-0.0574, 0.0191, -0.1066, 0.0168, 0.0367, -0.0239, -0.1018, -0.0542,
0.0154, 0.0090],
[ 0.0026, 0.0179, -0.0321, -0.0292, 0.0661, 0.0145, -0.1246, -0.1088,
0.0168, 0.0228],
[-0.0681, 0.0125, -0.0914, 0.0614, 0.0409, 0.0196, -0.0901, -0.0417,
0.0183, 0.0010],
[-0.0135, 0.0286, -0.0493, -0.0038, 0.0623, 0.0098, -0.1423, -0.0704,
0.0317, 0.0111],
[-0.0305, 0.0179, -0.0894, 0.0291, 0.0392, 0.0523, -0.1185, -0.0550,
0.0463, 0.0029],
[-0.0542, 0.0663, -0.0760, 0.0005, 0.0630, 0.0680, -0.1526, -0.0700,
0.0058, -0.0963],
[-0.0267, 0.0466, -0.0902, 0.0978, 0.0103, 0.0365, -0.1090, -0.0673,
0.0239, -0.0191],
[-0.0241, 0.0408, -0.0435, 0.0488, 0.0286, 0.0361, -0.0961, -0.0781,
0.0490, -0.0077],
[-0.0451, -0.0311, -0.0729, -0.0110, 0.0183, 0.0761, -0.1012, -0.0648,
0.0275, -0.0034]], device='cuda:0', grad_fn=<AddmmBackward0>)
Training MNIST¶
Our network takes an image (as a tensor) and outputs class probabilities.
- Need a loss
- Need an optimizer (e.g. SGD, ADAM)
backwarddoes not update parameters
In [174]:
batch[1]
Out[174]:
tensor([5, 0, 3, 7, 5, 5, 2, 7, 9, 1])
In [175]:
loss = F.cross_entropy(output,batch[1].to('cuda')) #combines log softmax and
loss
Out[175]:
tensor(2.3061, device='cuda:0', grad_fn=<NllLossBackward0>)
$$L(x,class) = - \log\left(\frac{e^{x_{\mathrm{class}}}}{\sum_j e^{x_j}}\right)$$
In [176]:
loss.backward() # sets grad, but does not change parameters of model
Training MNIST¶
Epoch - One pass through the training data.
In [177]:
import time
optimizer = torch.optim.Adam(model.parameters(), lr=0.00001) # need to tell optimizer what it is optimizing
losses = []
for epoch in range(10):
start = time.time()
for i, (img,label) in enumerate(train_loader):
optimizer.zero_grad() # IMPORTANT!
img, label = img.to('cuda'), label.to('cuda')
output = model(img)
loss = F.cross_entropy(output, label)
loss.backward()
optimizer.step()
losses.append(loss.item())
print(f"Epoch {epoch} took {time.time()-start}s")
Epoch 0 took 25.338215827941895s Epoch 1 took 25.018168926239014s Epoch 2 took 25.70171070098877s Epoch 3 took 25.158550262451172s Epoch 4 took 25.13508152961731s Epoch 5 took 25.4727680683136s Epoch 6 took 25.059509754180908s Epoch 7 took 25.239453315734863s Epoch 8 took 24.99835443496704s Epoch 9 took 25.514211654663086s
In [178]:
%%html
<div id="batchq" style="width: 500px"></div>
<script>
$('head').append('<link rel="stylesheet" href="https://bits.csb.pitt.edu/asker.js/themes/asker.default.css" />');
var divid = '#batchq';
jQuery(divid).asker({
id: divid,
question: "At iteration 100, how many images have gone through the neural network?",
answers: ["50","100","1000","5000","None of the above"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
In [179]:
plt.plot(losses); plt.xlabel('Iteration'); plt.ylabel('Loss');
This is the batch loss.
How can we make training faster?
$ nvidia-smi
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 525.85.12 Driver Version: 525.85.12 CUDA Version: 12.0 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 NVIDIA GeForce ... On | 00000000:17:00.0 Off | N/A |
| 23% 35C P8 9W / 250W | 1297MiB / 11264MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
| 1 NVIDIA TITAN RTX On | 00000000:65:00.0 Off | N/A |
| 41% 49C P2 93W / 280W | 247MiB / 24576MiB | 10% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
In [180]:
train_loader = torch.utils.data.DataLoader(train_data,batch_size=1024,shuffle=True,num_workers=8)
model = MyNet().to('cuda')
optimizer = torch.optim.Adam(model.parameters(), lr=0.00001) # need to tell optimizer what it is optimizing
losses = []
for epoch in range(10):
start = time.time()
for i, (img,label) in enumerate(train_loader):
optimizer.zero_grad() # IMPORTANT!
img, label = img.to('cuda'), label.to('cuda')
output = model(img)
loss = F.cross_entropy(output, label)
loss.backward()
optimizer.step()
losses.append(loss.item())
print(f"Epoch {epoch} took {time.time()-start}s")
Epoch 0 took 1.1977097988128662s Epoch 1 took 1.2670469284057617s Epoch 2 took 1.1980950832366943s Epoch 3 took 1.2358448505401611s Epoch 4 took 1.2233784198760986s Epoch 5 took 1.2111268043518066s Epoch 6 took 1.1942381858825684s Epoch 7 took 1.215287208557129s Epoch 8 took 1.1779179573059082s Epoch 9 took 1.1748261451721191s
In [181]:
%%html
<div id="batchcovq" style="width: 500px"></div>
<script>
$('head').append('<link rel="stylesheet" href="https://bits.csb.pitt.edu/asker.js/themes/asker.default.css" />');
var divid = '#batchcovq';
jQuery(divid).asker({
id: divid,
question: "Will you converge to the same loss with a larger batch size?",
answers: ["Yes","No","Maybe"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
In [182]:
plt.plot(losses); plt.xlabel('Iteration'); plt.ylabel('Loss');
Testing MNIST¶
In [183]:
correct = 0
with torch.no_grad(): #no need for gradients - won't be calling backward to clear them
for img, label in test_loader:
img, label = img.to('cuda'), label.to('cuda')
output = F.softmax(model(img),dim=1)
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(label.view_as(pred)).sum().item()
print("Accuracy",correct/len(test_loader.dataset))
Accuracy 0.8008
Smaller batch training yielded accuracy of 95%
Some Failures¶
*Not from this particular network
